# 5.1.1 探索性数据分析(EDA)
探索性数据分析(`EDA`)说白了就是通过可视化的方式来看看数据中特征与特征之间,特征与目标之间的潜在关系,看看有什么有用的线索可以挖掘,例如哪些数据是噪声,有哪些特征的相关性比较低,后续可以造出哪些新的特征等。
## 初窥
当然,在`EDA`之前先要加载数据,我们不妨先将训练集`train.csv`读到内存中,并看一看。
```python
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
data=pd.read_csv('./Titanic/train.csv')
# 看看data的前5行
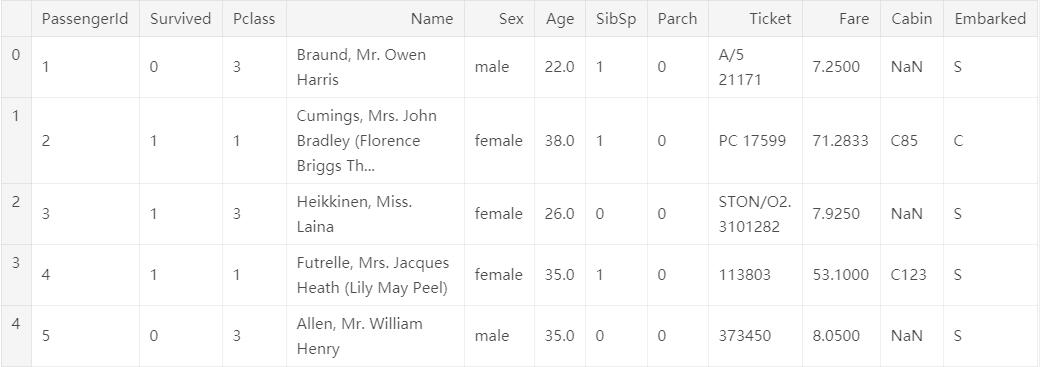
data.head()
```
从图中可以看出数据是由`11`个特征和`1`个标签(`Survived`)组成的。其中各个特征和标签的意义如下:
| 特征 | 意义 |
|:-:|:-:|
| Survived | 是否生还,1表示是,0表示否 |
| PassengerId| 乘客ID|
| Pclass| 船票类型, 总共3种类型:1(一等舱),2(二等舱),3(三等舱)|
| Name | 船客姓名|
| Sex | 船客性别:female,male|
| Age|船客年龄|
|SibSp|船客的兄弟姐妹妻子丈夫的数量|
|Parch|船客的父母,孩子的数量|
|Ticket|船票|
|Fare|船客在船上所花的钱|
|Cabin|船客的船舱号|
|Embarked|船客登船的口岸:C,Q,S|
了解了数据种各个属性的含义之后,我们可以看看这个数据集中有没有缺失值。
```python
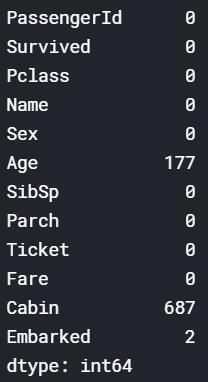
data.isnull().sum()
```
可以看出`Age`,`Cabin`和`Embarked`这三个特征中有缺失值,我们需要处理这些缺失值。怎样处理呢?先不着急,我们可以先看看数据中有哪些信息可以挖掘。
## 有多少人活了下来
我们首先可以看看训练集中有多少人活了下来。
```python
f,ax=plt.subplots(1,2,figsize=(18,8))
# 生还比例饼图
data['Survived'].value_counts().plot.pie(explode=[0,0.1],autopct='%1.1f%%',ax=ax[0],shadow=True)
ax[0].set_title('Survived')
ax[0].set_ylabel('')
# 生还数量直方图
sns.countplot('Survived',data=data,ax=ax[1])
ax[1].set_title('Survived')
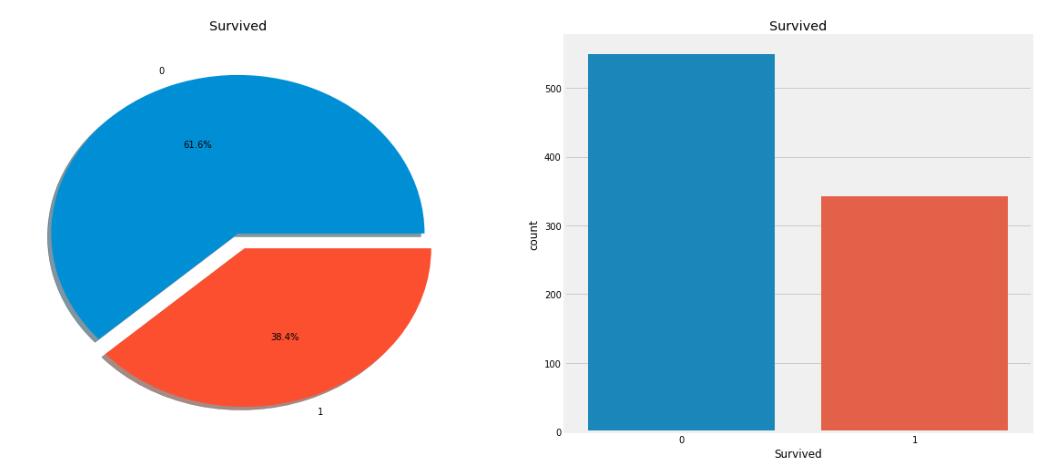
plt.show()
```
从图中可以看出泰坦尼克沉船事件中还是凶多吉少的。因为在`891`名船客中,只有约`38%`左右的人幸免于难,那么接下来尝试使用数据集中不同的特征,来看看他们的生还率有多少。其实这样一个过程可以看出大概有哪些类型的船客活了下来。
## 性别与生还率的关系
首先,看看不同性别的生还者数量。
```python
data.groupby(['Sex','Survived'])['Survived'].count()
```
看上去好像女性船客的生还率高一些,不妨再可视化一下。
```python
f,ax=plt.subplots(1,2,figsize=(18,8))
data[['Sex','Survived']].groupby(['Sex']).mean().plot.bar(ax=ax[0])
ax[0].set_title('Survived vs Sex')
sns.countplot('Sex',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Sex:Survived vs Dead')
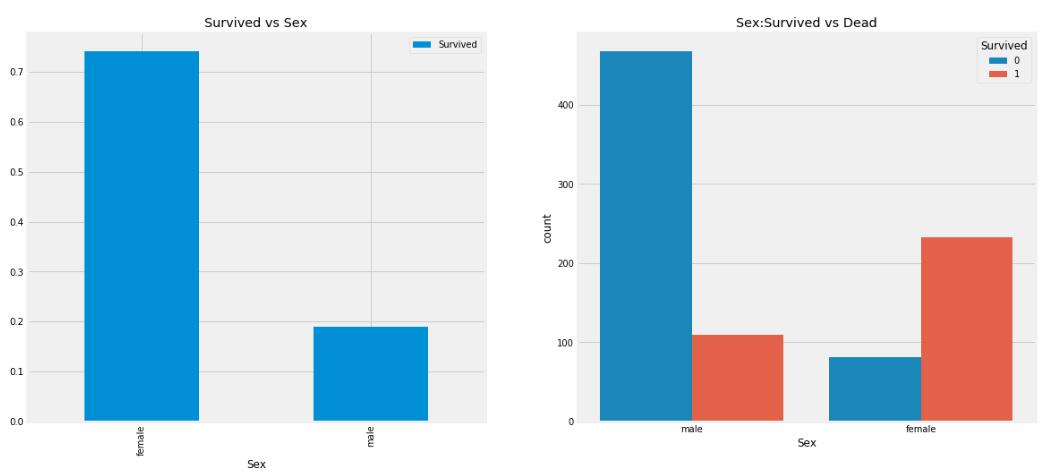
plt.show()
```
从图中可以看出一个比较有趣的现象,船上的男人是比女人多了`200`多人,但是女人生还的人数几乎是男人生还的人数的两倍,女人的存活率约为`75%`,而男人的存活率约为`19%`的样子。所以 `Sex`这个特征应该是一个能够很好的区分一个人是否生还的特征。而且对于生还来说,好像是女士优先。
## 船票类型与生还率的关系
船票类型分三个档次,其中`1`为一等舱,`2`为二等舱,`3`为三等舱。既然船舱分三六九等,那么是不是越高级的舱,它的生还率越高呢?
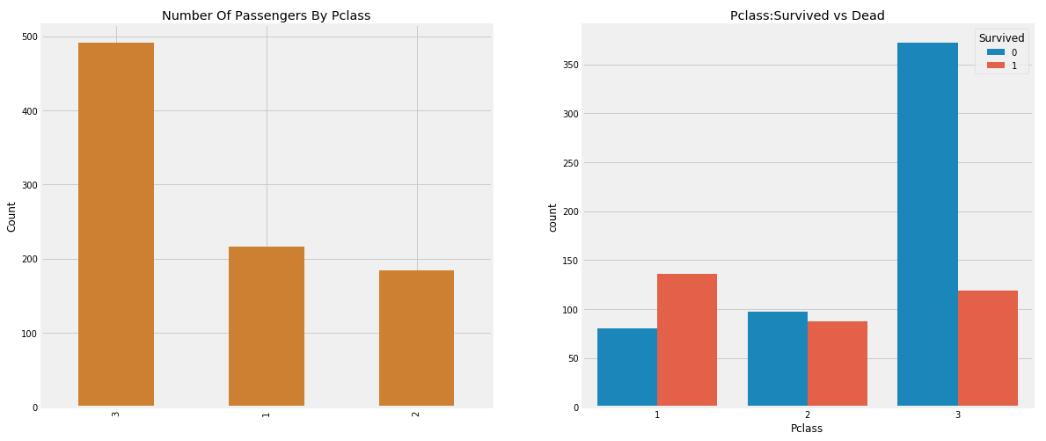
```python
f,ax=plt.subplots(1,2,figsize=(18,8))
data['Pclass'].value_counts().plot.bar(ax=ax[0])
ax[0].set_title('Number Of Passengers By Pclass')
ax[0].set_ylabel('Count')
sns.countplot('Pclass',hue='Survived',data=data,ax=ax[1])
ax[1].set_title('Pclass:Survived vs Dead')
plt.show()
```
虽然说钱不是万能的,但从可视化结果可以看出,一等舱的生还率最高,大于为`63%`,二等舱的生还率约为`48%` ,而且虽然三等舱的船客人数是最多的,但生还率确是最低的。所以不难看出,金钱地位还是很重要的,也许一等舱周围有比较多的救生设备。
## 上流女性与生还率的关系
从前两次可视化结果可以看出,女性,上流人士成为了是否能够活下来的关键,那么上流女性(两者的结合)的生还率会不会很高呢?
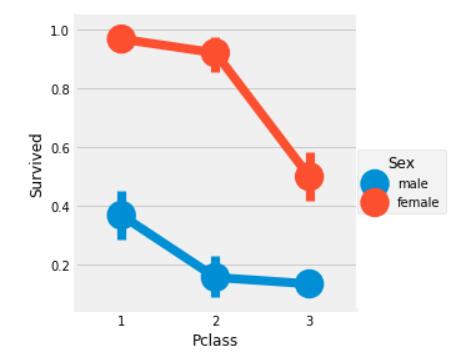
```python
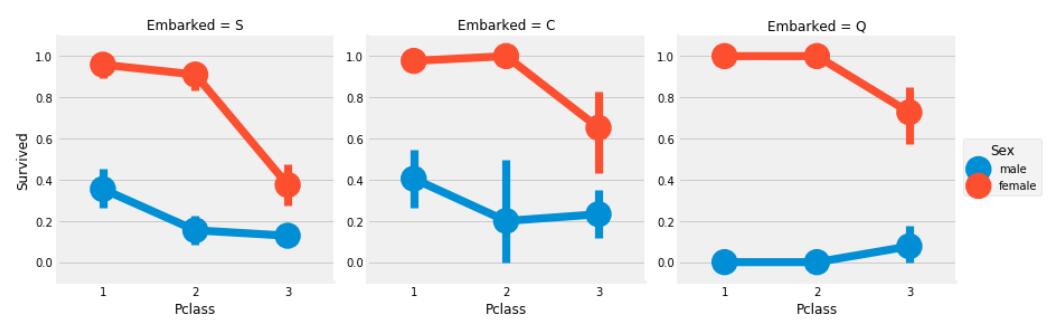
sns.factorplot('Pclass','Survived',hue='Sex',data=data)
plt.show()
```
从这张图可以看出一等舱的女性(上流女性)的生还率非常高!几乎接近了百分之百!而且二等舱和三等舱的女性的生还率也远比男性的生还率高。这也验证了我们的猜测,在沉船后是优先女性和一等舱的船客的。
## 年龄与生还率的关系
首先可以先看一下训练集中船客的年龄的最值和均值。
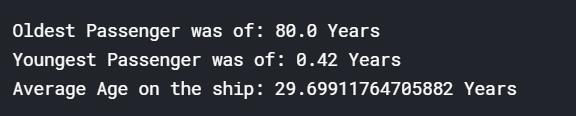
```python
print('Oldest Passenger was of:',data['Age'].max(),'Years')
print('Youngest Passenger was of:',data['Age'].min(),'Years')
print('Average Age on the ship:',data['Age'].mean(),'Years')
```
年纪最大的是`80`岁的老爷爷或者老太太,最小的是刚出生的小 `baby`,平均年龄快`30`岁。这个还是符合常理的。接下来我们看看船舱等级,年龄和生还率的关系,以及性别,年龄和生还率的关系。
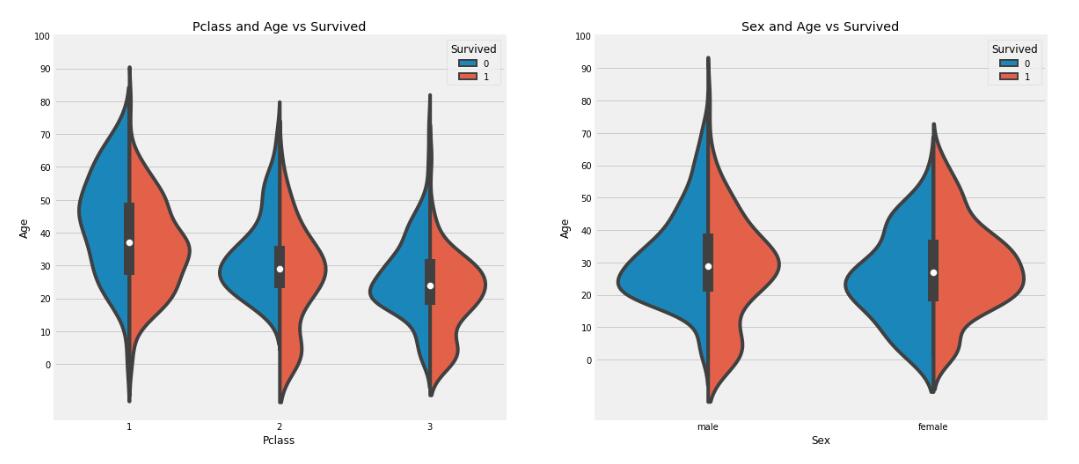
```python
f,ax=plt.subplots(1,2,figsize=(18,8))
sns.violinplot("Pclass","Age", hue="Survived", data=data,split=True,ax=ax[0])
ax[0].set_title('Pclass and Age vs Survived')
ax[0].set_yticks(range(0,110,10))
sns.violinplot("Sex","Age", hue="Survived", data=data,split=True,ax=ax[1])
ax[1].set_title('Sex and Age vs Survived')
ax[1].set_yticks(range(0,110,10))
plt.show()
```
从可视化结果可以看出:
- 儿童的数量随着船舱等级的增加而增加,`10`岁以下的小朋友存活率仿佛都还挺高的,跟船舱等级好像没有太大关系。
- 来自一等舱的`20-50`岁的船客的存活率很高,而且对女性的生还率一如既往的高。
- 对于男性来说,年纪越大,生还率越低。
不过我们的年龄是有缺失值的,如果图简单,可以使用平均年龄来填充缺失的年龄。但是这样做并不合适,比如人家只是个`5`岁的小屁孩,但是你把人家强行改成`29`岁显然是不合适的。那有没有能够更加准确地知道缺失的年龄是多少的方法呢?有!我们可以根据姓名来推断缺失的年龄,因为姓名中有很多类似`Mr`或者`Mrs`这样的前缀,所以我们可以根据姓名的前缀来填充缺失的年龄。
## 填充缺失年龄
外国人的姓名和我们中国人的姓名不太一样,一般都会有`Mr`、 `Mrs`、`Miss`、`Dr`等特殊前缀。所以我们可以先提取姓名中的前缀。
```python
data['Initial']=0
for _ in data:
data['Initial']=data.Name.str.extract('([A-Za-z]+)\.')
```
这样我们能够提取出诸如:`Capt`、`Col`、`Don`、`Lady`、`Major`、`Sir`等前缀,接着我们可以将这些前缀替换成`Miss`、`Mr`、`Mrs`、`Other`这四个类别,并统计这四个类别的平均年龄。
```python
data['Initial'].replace(['Mlle','Mme','Ms','Dr','Major','Lady','Countess','Jonkheer','Col','Rev','Capt','Sir','Don'],['Miss','Miss','Miss','Mr','Mr','Mrs','Mrs','Other','Other','Other','Mr','Mr','Mr'],inplace=True)
data.groupby('Initial')['Age'].mean()
```
接着可以根据前缀来填充缺失的年龄。
```python
data.loc[(data.Age.isnull())&(data.Initial=='Mr'),'Age']=33
data.loc[(data.Age.isnull())&(data.Initial=='Mrs'),'Age']=36
data.loc[(data.Age.isnull())&(data.Initial=='Miss'),'Age']=22
data.loc[(data.Age.isnull())&(data.Initial=='Other'),'Age']=46
```
填充完缺失值后,可以尝试可视化一下。
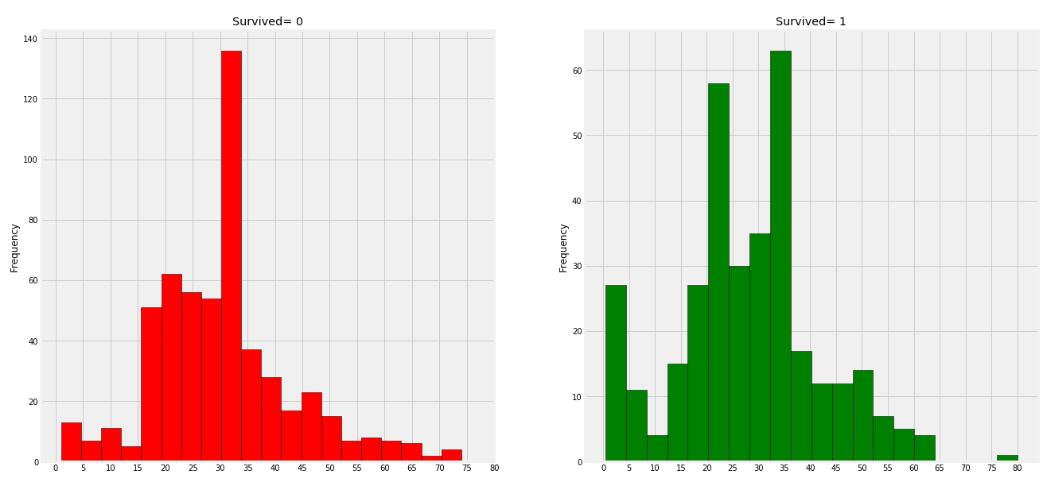
```python
f,ax=plt.subplots(1,2,figsize=(20,10))
data[data['Survived']==0].Age.plot.hist(ax=ax[0],bins=20,edgecolor='black',color='red')
ax[0].set_title('Survived= 0')
x1=list(range(0,85,5))
ax[0].set_xticks(x1)
data[data['Survived']==1].Age.plot.hist(ax=ax[1],color='green',bins=20,edgecolor='black')
ax[1].set_title('Survived= 1')
x2=list(range(0,85,5))
ax[1].set_xticks(x2)
plt.show()
```
从图中可以看出`5`岁以下的小屁孩的生还率比较高,`80`岁的老人活下来了。
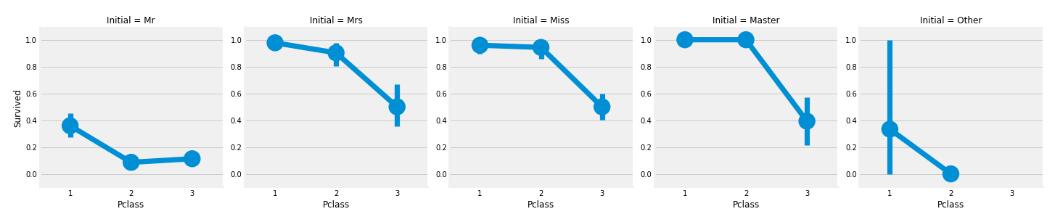
```python
sns.factorplot('Pclass','Survived',col='Initial',data=data)
plt.show()
```
嗯,女性和小孩的生还率比较高。
## 登船口岸与生还率的关系
先把口岸和生还率的关系画出来。
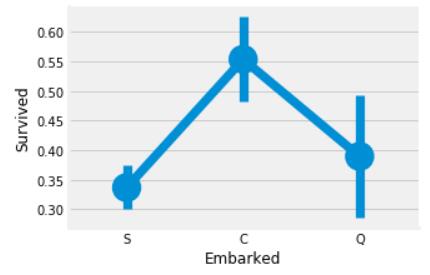
```python
sns.factorplot('Embarked','Survived',data=data)
fig=plt.gcf()
fig.set_size_inches(5,3)
plt.show()
```
可以看出从`C`号口岸上船的生还率最高,最低的是`S`号口岸。嗯,好像并没有什么线索,我们可以再深入一点。
```python
f,ax=plt.subplots(2,2,figsize=(20,15))
sns.countplot('Embarked',data=data,ax=ax[0,0])
ax[0,0].set_title('No. Of Passengers Boarded')
sns.countplot('Embarked',hue='Sex',data=data,ax=ax[0,1])
ax[0,1].set_title('Male-Female Split for Embarked')
sns.countplot('Embarked',hue='Survived',data=data,ax=ax[1,0])
ax[1,0].set_title('Embarked vs Survived')
sns.countplot('Embarked',hue='Pclass',data=data,ax=ax[1,1])
ax[1,1].set_title('Embarked vs Pclass')
plt.subplots_adjust(wspace=0.2,hspace=0.5)
plt.show()
```
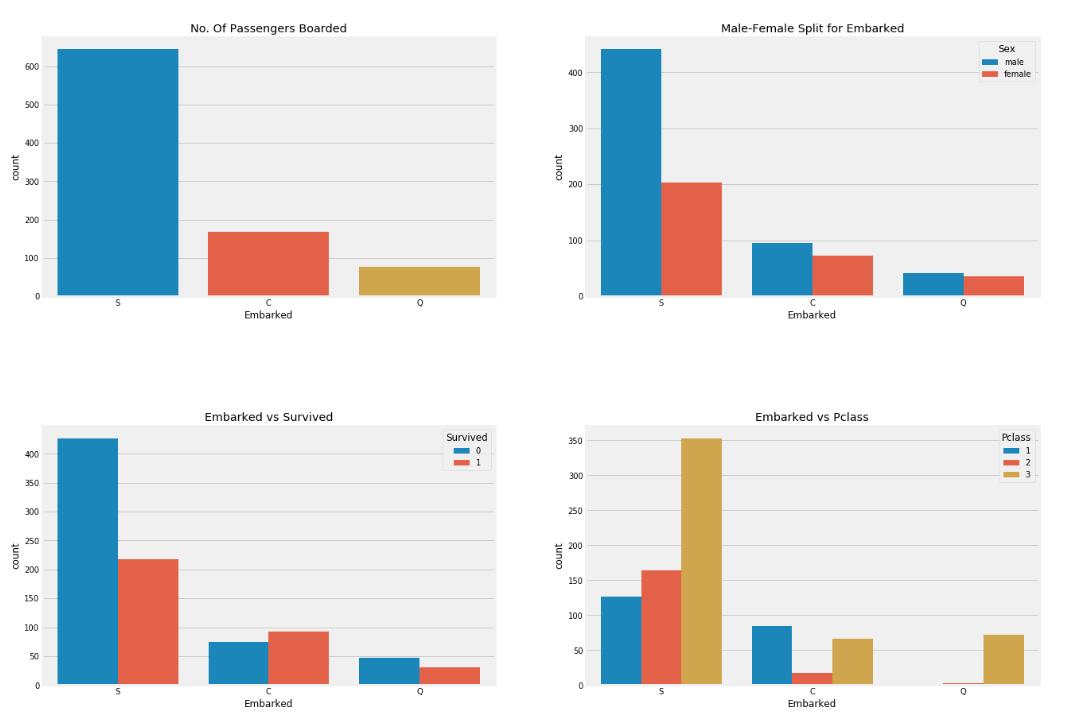
现在能看出很多信息了:
- 上船人数最多的口岸是`S`号口岸,而且在`S`号口岸上船的人大多数都是三等舱的船客。
- `C`号口岸上船的生还率最高,可能大部分`C`口岸上船的人是一等舱和二等舱船客吧。
- 虽然有很多一等舱的土豪们基本上都是在`S`口岸上船的,但是 `S`口岸的的生还率最低。这是因为`S`口岸上船的人中有很多都是三等舱的船客。
- `Q`号口岸上船的人中有`90%`多都是三等舱的船客。
```python
sns.factorplot('Pclass','Survived',hue='Sex',col='Embarked',data=data)
plt.show()
```
我们可以看出:
- 一等舱和二等舱的女性的生还率几乎为`100%`, 这与女性是一等舱还是二等舱没啥关系。
- `S`号口岸上船并且是三等舱的,不管是男的还是女的,生还率都很低。金钱决定命运。
- `Q`号口岸上船的男性几乎团灭,因为`Q`号口岸上船的基本上都是三等舱船客。
## 填充缺失口岸
由于大多数人都是从`S`号口岸上的船,我们可以假设由于人多,所以在`S`口岸登记信息时漏了几位船客,所以不妨用`S`号口岸填充缺失值。
```python
data['Embarked'].fillna('S',inplace=True)
```
## 兄弟姐妹的数量与生还率的关系
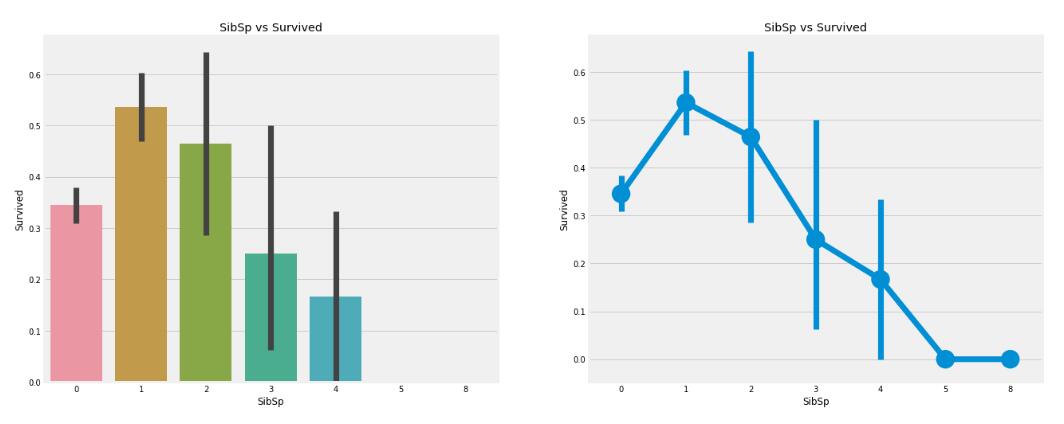
```python
f,ax=plt.subplots(1,2,figsize=(20,8))
sns.barplot('SibSp','Survived',data=data,ax=ax[0])
ax[0].set_title('SibSp vs Survived')
sns.factorplot('SibSp','Survived',data=data,ax=ax[1])
ax[1].set_title('SibSp vs Survived')
plt.close(2)
plt.show()
```
从图可以看出,如果一位船客是单独一个人上船旅游,没有兄弟姐妹而且是单身,那么他有大约`34%`的生还率,生还率比较低。如果兄弟姐妹的数量变多,那么生还率还是呈下降趋势的。这其实挺合理的,因为如果是一个家庭在船上的话,可能会设法救他们而不是救自己,这样一来可能谁都救不了。
## 父母的数量与生还率的关系
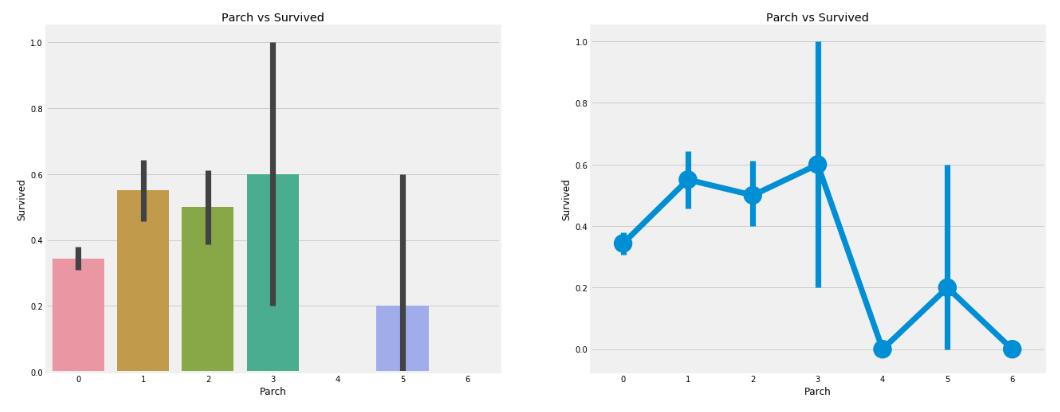
```python
f,ax=plt.subplots(1,2,figsize=(20,8))
sns.barplot('Parch','Survived',data=data,ax=ax[0])
ax[0].set_title('Parch vs Survived')
sns.factorplot('Parch','Survived',data=data,ax=ax[1])
ax[1].set_title('Parch vs Survived')
plt.close(2)
plt.show()
```
从图上看会发现结果和上面的比较相似,父母在船上的船客有更大的生还机会。而且对于那些在船上有`1-3`个父母的人来说,生还率还是比较高的。
## 花费与生还率的关系
首先,先看一下花费的最值和均值。
```python
print('Highest Fare was:',data['Fare'].max())
print('Lowest Fare was:',data['Fare'].min())
print('Average Fare was:',data['Fare'].mean())
```
惊奇的发现,居然有人可以享受免费豪华邮轮!!!!
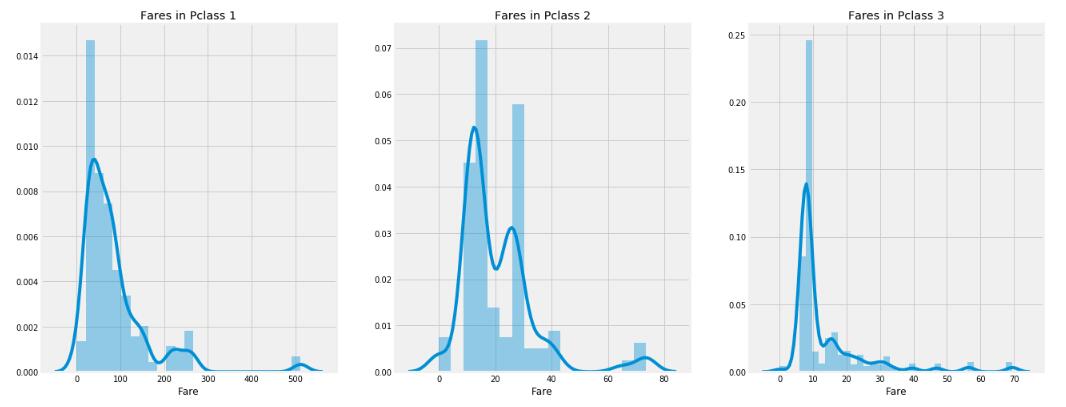
```python
f,ax=plt.subplots(1,3,figsize=(20,8))
sns.distplot(data[data['Pclass']==1].Fare,ax=ax[0])
ax[0].set_title('Fares in Pclass 1')
sns.distplot(data[data['Pclass']==2].Fare,ax=ax[1])
ax[1].set_title('Fares in Pclass 2')
sns.distplot(data[data['Pclass']==3].Fare,ax=ax[2])
ax[2].set_title('Fares in Pclass 3')
plt.show()
```
从图中可以看出平均花费其实是二等舱的普遍消费水平,但是三等舱的人数是最多的,而三等舱的人群中花费人数最多的是`10`左右,因此平均`32`的花费是被有钱的大佬给提上去的。
## 简单总结一下
看了这么多特征对于生还的影响,可能有点懵,不妨先简单总结一下根据可视化结果所获得的信息。
- 性别:女性的生还率高。
- 船舱等级:越有钱越容易活下来,头等舱的生还率最高,三等舱的生还率最低。
- 年龄:`10`岁以下的小朋友的存活率比较高,`15-35`岁的年轻人存活率低。可能年轻人就是炮灰吧。
- 口岸:即使大多数一等舱的船客在`S`号口岸上的船, 但生还率不是最高的。`Q`号口岸的基本上是三等舱的船客。
- 兄弟姐妹父母爱人数量:有`1-2`个兄弟姐妹,配偶在船上,或 `1-3`个父母的生还率比较高,独自一人或者一个大家庭都在船上的生还率比较低。
## 特征之间的相关性系数
相关性分为正相关与负相关,正相关指的是:如果特征`A`的数值变大会导致特征`B`的数值变大;负相关指的是:如果特征`A`的数值变小会导致特征`B`的数值变大。通常使用`[-1, 1]`的数值来表示两个特征之间的相关性,这个值称为**相关性系数**。若该系数为`1`那么表示两个特征之间完全正相关,若为`-1`则表示完全负相关,若为`0`则表示两个特征之间没有相关性(线性的)。
如果现在两个特征高度相关或者完全相关,这就意味着这两个特征都包含高度相似的信息,并且信息的差异非常小,所以其中一个特征是多余的。在构建模型时,我们应该尽量消除这种多余的特征,因为这样能减少训练的时间,也可以在某种程度上缓解过拟合。
所以接下来用热力图对相关性系数进行可视化。
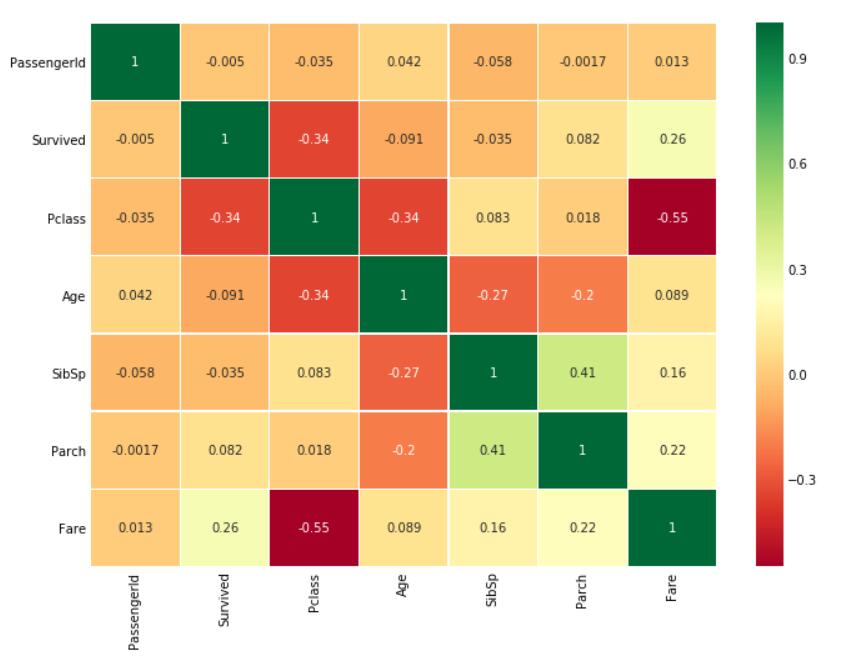
```python
sns.heatmap(data.corr(),annot=True,cmap='RdYlGn',linewidths=0.2) #data.corr()-->correlation matrix
fig=plt.gcf()
fig.set_size_inches(10,8)
plt.show()
```
从热力图上可以看出这些特征之间没有太大的相关性,最高的也就 `SibSp`与`Parch`,值为`0.41`。