# 支持向量机
## 线性可分支持向量机
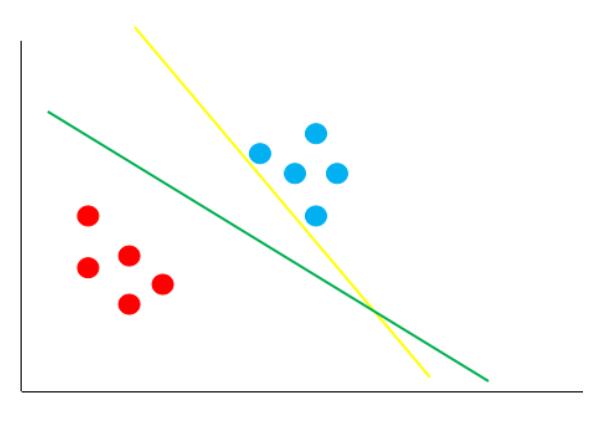
例如逻辑回归这种广义线性模型对数据进行分类时,其实本质就是找到一条 **决策边界** ,然后将数据分成两个类别(边界的一边是一种类别,另一边是另一种类别)。如下图中的两条线是两种模型产生的 **决策边界** :
图中的绿线与黄线都能很好的将图中的红点与蓝点给区分开。但是,哪条线的泛化性更好呢?可能你不太了解泛化性,也就是说,我们的这条直线,不仅需要在训练集 **(已知的数据)** 上能够很好的将红点跟蓝点区分开来,还要在测试集 **(未知的数据)** 上将红点和蓝点给区分开来。
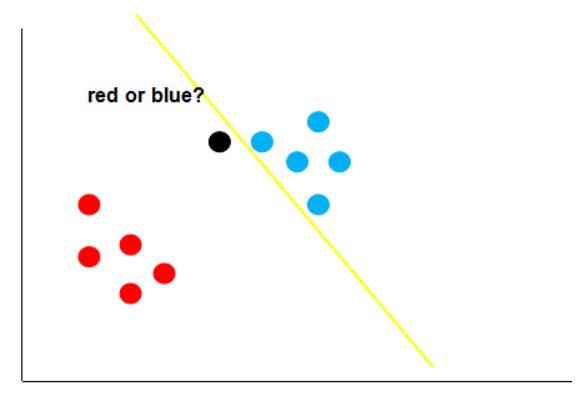
假如经过训练,我们得到了黄色的这条决策边界用来区分我们的数据,这个时候又来了一个数据,即黑色的点,那么你觉得黑色的点是属于红的这一类,还是蓝色的这一类呢?
如上图,根据黄线的划分标准,黑色的点应该属于红色这一类。可是,我们肉眼很容易发现,黑点离蓝色的点更近,它应该是属于蓝色的点。这就说明,黄色的这条直线它的泛化性并不好,它对于未知的数据并不能很好的进行分类。那么,如何得到一条泛化性好的直线呢?这个就是支持向量机考虑的问题。
### 基本思想
支持向量机的思想认为,一条决策边界它如果要有很好的泛化性,它需要满足一下以下两个条件:
- 能够很好的将样本划分
- 离最近的样本点最远
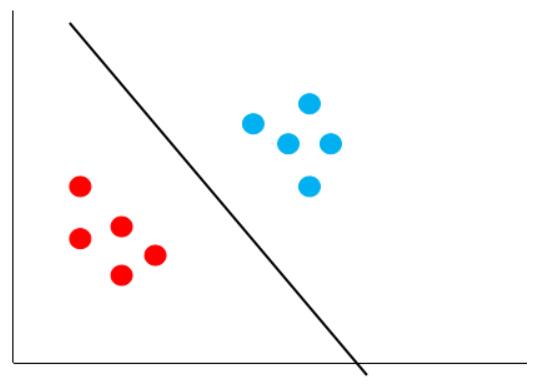
比如下图中的黑线:
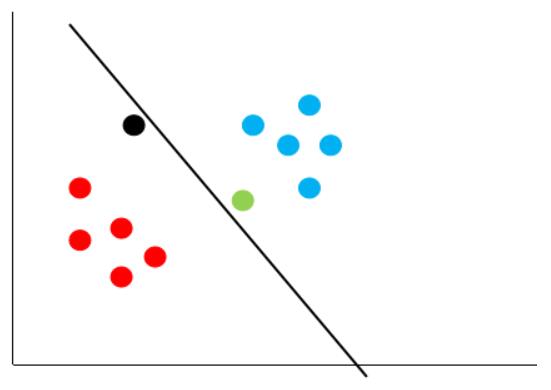
它能够正确的将红点跟蓝点区分开来,而且,它还保证了对未知样本的容错率,因为它离最近的红点跟蓝点都很远,这个时候,再来一个数据,就不会出现之前黄色决策边界的错误了。
无论新的数据出现在哪个位置,黑色的决策边界都能够很好的给它进行分类,这个就是支持向量机的基本思想。
### 间隔与支持向量
在样本空间中,决策边界可以通过如下线性方程来描述:
$$
w^Tx+b=0
$$
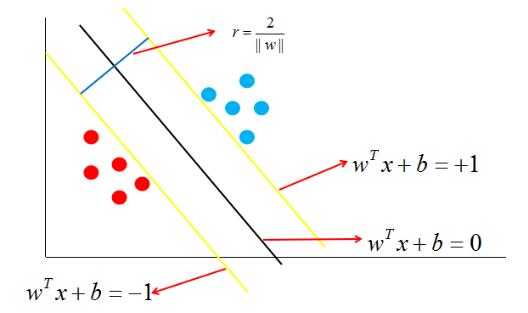
其中$$w=(w_1,w_2,..,w_d)$$为法向量,决定了决策边界的方向。$$b$$为位移项,决定了决策边界与原点之间的距离。显然,决策边界可被法向量和位移确定,我们将其表示为$$(w,b)$$。样本空间中的任意一个点$$x$$,到决策边界$$(w,b)$$的距离可写为:
$$
r=\frac{|w^Tx+b|}{||w||}
$$
假设决策边界##(w,b)$$能够将训练样本正确分类,即对于任何一个样本点$$(x_i,y_i)$$,若它为正类,即$$y_i=+1$$时,$$w^Tx+b\geq +1$$。若它为负类,即$$y_i=-1$$时,$$w^Tx+b\leq -1$$。
如图中,距离最近的几个点使两个不等式的等号成立,它们就被称为**支持向量**,即图中两条黄色的线。两个异类支持向量到超平面的距离之和为:
$$
r=\frac{2}{||w||}
$$
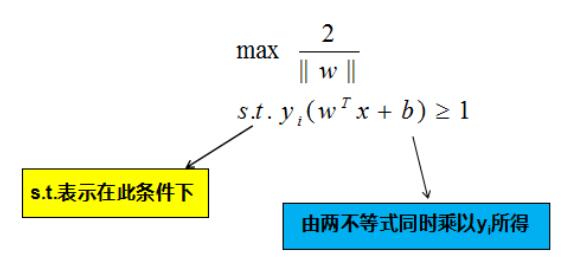
它被称为**间隔**,即蓝线的长度。欲找到具有“最大间隔”的决策边界,即黑色的线,也就是要找到能够同时满足如下式子的$$w$$与$$b$$:
显然,为了最大化间隔,仅需最大化$$||w||^{-1}$$,这等价于最小化$$||w||^2$$,于是,条件可以重写为:
$$
min \frac{1}{2}||w||^2
$$
$$
s.t. y_i(w^Tx+b)\geq1
$$
这就是线性可分支持向量机的基本型。
### 对偶问题
我们已经知道了支持向量机的基本型,问题本身是一个凸二次规划问题,可以用现成的优化计算包求解,不过可以用更高效的方法。支持向量机的模型如下:
$$
min\frac{1}{2}||W||^2
$$
$$
s.t. y_i(w^Tx+b)\geq1
$$
对两式子使用拉格朗日乘子法可得到其**对偶问题**。具体为,对式子的每条约束添加拉格朗日乘子$$\alpha\geq0$$,则该问题的拉格朗日函数可写为:
$$
L(w,b,\alpha)=\frac{1}{2}||w||^2+\sum^m_{i=1}\alpha_i(1-y_i(w^Tx_i+b))......(1)
$$
其中$$\alpha=(\alpha_1,\alpha_2,..,\alpha_m)$$。令$$L(w,b,\alpha)$$对$$w$$和$$b$$的偏导为零可得:
$$
w=\sum_{i=1}^m\alpha_iy_ix_i......(2)
$$
$$
0=\sum_{i=1}^m\alpha_iy_i......(3)
$$
将式子$$2$$带入式子$$1$$,则可将$$w$$和$$b$$消去,再考虑式子$$3$$的约束,就可得到原问题的**对偶问题** :
$$
max(\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j)
$$
$$
s.t. \sum_{i=1}^m\alpha_iy_i=0
$$
$$
\alpha_i\geq0
$$
解出$$\alpha$$后,求出`w`与`b`即可得到模型:
$$
f(x)=w^Tx+b=\sum_{i=1}^m\alpha_iy_ix_i^Tx+b......(4)
$$
从对偶问题解出的$$\alpha_i$$是拉格朗日乘子,它恰对应着训练样本$$(x_i,y_i)$$,由于原问题有不等式的约束,因此上述过程需满足**KKT(Karush-Kuhn-Tucker)**条件,即要求:
$$
\begin{cases}
\alpha_i\geq0\\
y_if(x_i)-1\geq0\\
\alpha_i(y_if(x_i)-1)=0
\end{cases}
$$
于是,对任意训练样本$$(x_i,y_i)$$,总有$$\alpha_i=0$$或$$y_if(x_i)=1$$。若$$\alpha_i=0$$,则该样本将不会出现在式子`4`中,也就不会对$$f(x)$$,有任何影响。若$$\alpha_i>0$$,则必有$$y_if(x_i)=1$$,所对应的样本点位于最大间隔边界上,是一个支持向量。这显示出支持向量机的一个重要性质:**训练完后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关**。
##线性支持向量机
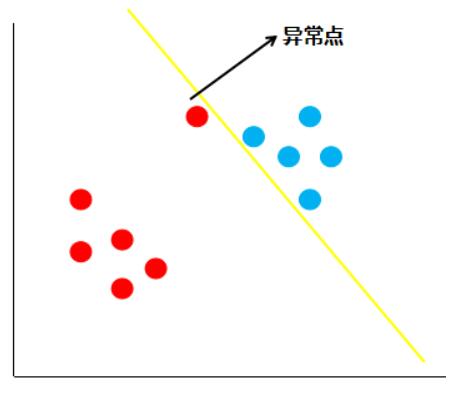
假如现在有一份数据分布如下图:
按照线性可分支持向量机的思想,黄色的线就是最佳的决策边界。很明显,这条线的泛化性不是很好,造成这样结果的原因就是数据中存在着异常点,那么如何解决这个问题呢,支持向量机引入了**软间隔最大化**的方法来解决。
所谓的**软间隔**,是相对于硬间隔说的,刚刚在**间隔与支持向量**中提到的间隔就是硬间隔。
接着我们再看如何可以软间隔最大化呢?SVM 对训练集里面的每个样本$$(x_i,y_i)$$引入了一个松弛变量$$\xi_i\geq0$$,使函数间隔加上松弛变量大于等于$$1$$,也就是说:
$$
y_i(w^Tx+b)\geq1-\xi
$$
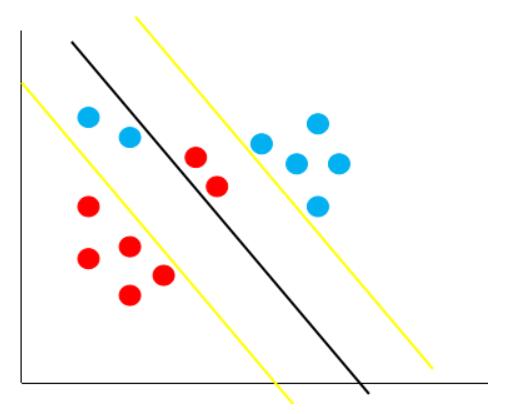
对比硬间隔最大化,可以看到我们对样本到超平面的函数距离的要求放松了,之前是一定要大于等于$$1$$,现在只需要加上一个大于等于$$0$$的松弛变量能大于等于$$1$$就可以了。也就是允许支持向量机在一些样本上出错,如下图:
当然,松弛变量不能白加,这是有成本的,每一个松弛变量$$\xi_i$$, 对应了一个代价$$\xi_i$$,这个就得到了我们的**软间隔最大化的支持向量机**,模型如下:
$$
min \frac{1}{2}||w||^2+C\sum^{m}_{i=1}\xi_i
$$
$$
s.t. y_i(w^Tx_i+b)\geq1-\xi_i
$$
$$
\xi_i\geq0
$$
这里,$$C>0$$为惩罚参数,可以理解为我们一般回归和分类问题正则化时候的参数。$$C$$越大,对误分类的惩罚越大,$$C$$越小,对误分类的惩罚越小。也就是说,我们希望权值的二范数尽量小,误分类的点尽可能的少。$$C$$是协调两者关系的正则化惩罚系数。在实际应用中,需要调参来选择。
同样的,使用**拉格朗日函数**将软间隔最大化的约束问题转化为无约束问题,利用相同的方法得到数学模型:
$$
max(\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j)
$$
$$
s.t. \sum_{i=1}^m\alpha_iy_i=0
$$
$$
0\leq\alpha_i\leq C
$$
这就是软间隔最大化时的**线性支持向量机**的优化目标形式,和之前的硬间隔最大化的线性可分支持向量机相比,我们仅仅是多了一个约束条件:
$$
0\leq\alpha_i\leq C
$$
##smo算法
**序列最小优化算法** ($$smo$$算法)是一种启发式算法, $$SVM$$中的模型参数可以使用该算法进行求解。其基本思路是:如果所有变量的解都满足此最优化问题的$$KKT$$条件,那么这个最优化问题的解就得到了。因为$$KKT$$条件是该最优化问题的充分必要条件。否则,选择两个变量,固定其他变量,针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解,因为这会使得原始二次规划问题的目标函数值变得更小。重要的是,这时子问题可以通过解析方法求解,这样就可以大大提高整个算法的计算速度。子问题有两个变量,一个是违反$$KKT$$条件最严重的那一个,另一个由约束条件自动确定。如此,$$smo$$算法将原问题不断分解为子问题并对子问题求解,进而达到求解原问题的目的。具体如下:
选择两个变量$$\alpha_1,\alpha_2$$,其它变量$$\alpha_i,i=3,4,..m$$是固定的。
于是,$$smo$$的最优化问题的子问题可以写成:
$$
min(\frac{1}{2}k_{11}\alpha_1^2+\frac{1}{2}k_{22}\alpha2^2+y_1y_2k_{12}\alpha_1\alpha_2-(\alpha_1+\alpha_2)+y_1\alpha_1\sum_{i=3}^my_i\alpha_ik_{i1}+y_2\alpha_2\sum_{i=3}^my_i\alpha_ik_{i2})
$$
$$
s.t. \alpha_1y_1+\alpha_2y_2=-\sum_{i=3}^my_i\alpha_i=\xi
$$
$$
0\leq\alpha_i\leq C,i=1,2
$$
其中:$$k_{ij}=k(x_i,x_j)$$
###smo算法目标函数的优化
为了求解上面含有这两个变量的目标优化问题,我们首先分析约束条件,所有的$$\alpha_1,\alpha_2$$都要满足约束条件,然后在约束条件下求最小。
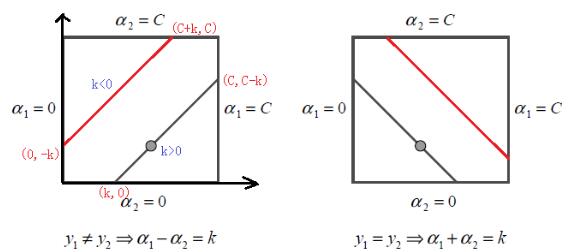
根据上面的约束条件$$\alpha_1y_1+\alpha_2y_2=\xi,0\leq\alpha_i\leq C,i=1,2$$,又由于$$y_1,y_2$$均只能取值$$1$$或者$$-1$$, 这样$$\alpha_1,\alpha_2$$在$$[0,C]$$和$$[0,C]$$形成的盒子里面,并且两者的关系直线的斜率只能为$$1$$或者$$-1$$,也就是说$$\alpha_1,\alpha_2$$的关系直线平行于$$[0,C]$$和$$[0,C]$$形成的盒子的对角线,如下图所示:
由于$$\alpha_1,\alpha_2$$的关系被限制在盒子里的一条线段上,所以两变量的优化问题实际上仅仅是一个变量的优化问题。不妨我们假设最终是$$\alpha_2$$的优化问题。由于我们采用的是启发式的迭代法,假设我们上一轮迭代得到的解是$$\alpha^{old}_1,\alpha^{old}_2$$,假设沿着约束方向$$\alpha_2$$未经剪辑的解是$$\alpha_2^{new,unc}$$。本轮迭代完成后的解为$$\alpha^{new}_1,\alpha^{new}_2$$。
由于$$\alpha_2^{new}$$必须满足上图中的线段约束。假设$$L$$和$$H$$分别是上图中$$\alpha_2^{new}$$所在的线段的边界。那么很显然我们有:
$$
L\leq\alpha_2^{new}\leq H
$$
而对于$$L$$和$$H$$,我们也有限制条件如果是上面左图中的情况,则:
$$
L=max(0,\alpha^{old}_2-\alpha^{old}_1),H=min(C,C+\alpha^{old}_2-\alpha^{old}_1)
$$
如果是上面右图中的情况,我们有:
$$
L=max(0,\alpha^{old}_2+\alpha^{old}_1-C),H=min(C,\alpha^{old}_2+\alpha^{old}_1)
$$
也就是说,假如我们通过求导得到的$$\alpha_2^{new,unc}$$,则最终的$$\alpha_2^{new}$$应该为:
$$
\alpha_2^{new,unc}=\begin{cases}
H,\alpha_2^{new,unc}>H\\
\alpha_2^{new,unc},L\leq\alpha_2^{new,unc}\leq H\\
L,\alpha_2^{new,unc}< L
\end{cases}
$$
那么如何求出$$\alpha_2^{new}$$呢?很简单,我们只需要将目标函数对$$\alpha2$$求偏导数即可。首先我们整理下我们的目标函数。为了简化叙述,我们令:
$$
E_i=g(x_i)-y_i
$$
其中:
$$
g(x)=w.\varnothing(x)+b
$$
$$
v_i=g(x_i)-\sum_{j=1}^2y_j\alpha_jk(x_i,x_j)-b
$$
最终可以计算得:
$$
\alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{k_{11}+k_{22}-2k_{12}}
$$
###smo算法两个变量的选择
$$smo$$算法需要选择合适的两个变量做迭代,其余的变量做常量来进行优化,那么怎么选择这两个变量呢?
一般来说,我们首先选择违反$$0 < \alpha_i < C$$这个条件的点。如果这些支持向量都满足$$KKT$$条件,再选择违反$$\alpha_i=0$$和$$\alpha_i=C$$的点。
$$smo$$算法称选择第二一个变量为内层循环,假设我们在外层循环已经找到了$$\alpha_1$$, 第二个变量$$\alpha_2$$的选择标准是让$$|E_1−E_2|$$有足够大的变化。由于$$\alpha_1$$定了的时候,$$E_1$$也确定了,所以要想$$|E_1−E_2|$$最大,只需要在$$E_1$$为正时,选择最小的$$E_i$$作为`E2`, 在$$E_1$$为负时,选择最大的$$E_i$$作为$$E_2$$,可以将所有的$$E_i$$保存下来加快迭代。
如果内存循环找到的点不能让目标函数有足够的下降, 可以采用遍历支持向量点来做$$\alpha_2$$,直到目标函数有足够的下降, 如果所有的支持向量做$$\alpha_2$$都不能让目标函数有足够的下降,可以跳出循环,重新选择$$\alpha_1$$。
###计算阈值b和差值Ei
在每次完成两个变量的优化之后,需要重新计算阈值$$b$$。当$$0<\alpha_1^{new}< C$$时,我们有:
$$
y_1-\sum_{i=1}^m\alpha_iy_ik_{i1}-b_1=0
$$
于是新的$$b_1^{new}$$为:
$$
b_1^{new}=y_1-\sum_{i=3}^m\alpha_iy_ik_{i1}-\alpha_1^{new}y_1k_{11}-\alpha2^{new}y_2k_{21}
$$
用$$E_1$$表示为:
$$
b_1^{new}=-E_1-y_1k_{11}(\alpha_1^{new}-\alpha_1^{old})-y_2k_{21}(\alpha_2^{new}-\alpha_2^{old})-b^{old}
$$
同样的,如果$$0<\alpha_2^{new}< C$$,则:
$$
b_2^{new}=-E_2-y_1k_{12}(\alpha_1^{new}-\alpha_1^{old})-y_2k_{22}(\alpha_2^{new}-\alpha_2^{old})-b^{old}
$$
最终:
$$
b^{new}=\frac{b^{new}_1+b^{new}_2}{2}
$$
继续更新得:
$$
E_i=\sum_sy_j\alpha_jk(x_i,x_j)+b^{new}-y_i
$$
其中$$s$$为所有支持向量$$x_j$$的集合。
###序列最小优化算法流程
`1`.取初始值$$\alpha^0=0,k=0$$
`2`.计算$$\alpha_2^{new,unc}$$,即:
$$
\alpha_2^{new,unc}=\alpha_2^{old}+\frac{y_2(E_1-E_2)}{k_{11}+k_{22}-2k_{12}}
$$
`3`.计算$$\alpha_2^{k+1}$$,即:
$$
\alpha_2^{k+1}=\begin{cases}
H,\alpha_2^{new,unc}>H\\
\alpha_2^{new,unc},L\leq\alpha_2^{new,unc}\leq H\\
L,\alpha_2^{new,unc}< L
\end{cases}
$$
`4`.利用$$\alpha_2^{k+1}$$和$$\alpha_1^{k+1}$$关系求出$$\alpha_1^{k+1}$$
`5`.计算$$b^{k+1}$$和$$E_i$$
`6`.在精度范围内检查是否满足如下的终止条件:
$$
\sum_{i=1}^m\alpha_iy_i=0
0\leq\alpha_i\leq C
\alpha_i^{k+1}=0
0<\alpha_i^{k+1}
`7`.如果满足则结束,返回$$\alpha^{k+1}$$,否则转向步骤`2`