以距离为尺-AGNES算法
AGNES 算法是一种聚类算法,最初将每个对象作为一个簇,然后这些簇根据某些距离准则被一步步地合并。两个簇间的相似度有多种不同的计算方法。聚类的合并过程反复进行直到所有的对象最终满足簇数目。所以理解 AGNES 算法前需要先理解一些距离准则。
距离准则
为什么需要距离
AGNES 算法是一种自底向上聚合的层次聚类算法,它先会将数据集中的每个样本看作一个初始簇,然后在算法运行的每一步中找出距离最近的两个簇进行合并,直至达到预设的簇的数量。所以AGNES算法需要不断的计算簇之间的距离,这也符合聚类的核心思想(物以类聚,人以群分),因此怎样度量两个簇之间的距离成为了关键。
距离的计算
衡量两个簇之间的距离通常分为最小距离、最大距离和平均距离。在 AGNES 算法中可根据具体业务选择其中一种距离作为度量标准。
最小距离
最小距离描述的是两个簇之间距离最近的两个样本所对应的距离。例如下图中圆圈和菱形分别代表两个簇,两个簇之间离得最近的样本的欧式距离为 3.3 ,则最小距离为 3.3。
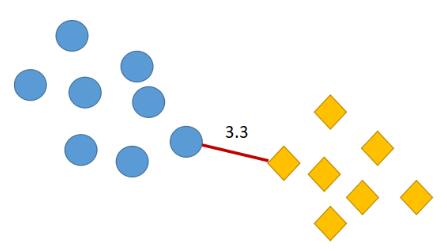
假设给定簇与,则最小距离为:
最大距离
最大距离描述的是两个簇之间距离最远的两个样本所对应的距离。例如下图中圆圈和菱形分别代表两个簇,两个簇之间离得最远的样本的欧式距离为 23.3 ,则最大距离为 23.3 。
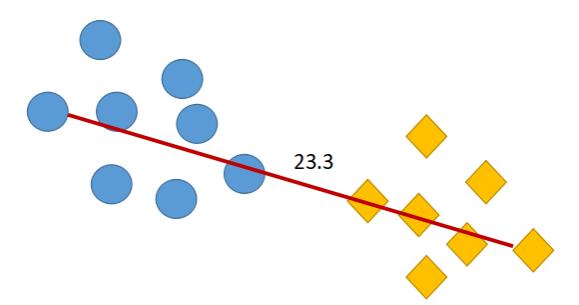
假设给定簇与,则最大距离为:
平均距离
平均距离描述的是两个簇之间样本的平均距离。例如下图中圆圈和菱形分别代表两个簇,计算两个簇之间的所有样本之间的欧式距离并求其平均值。
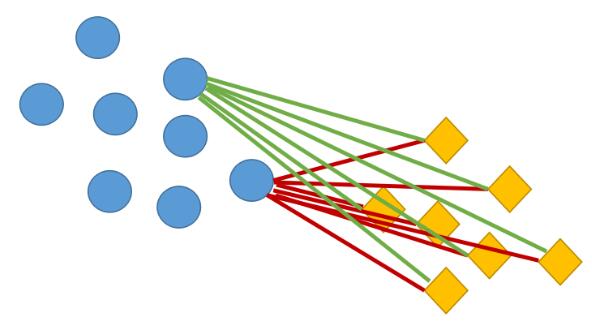
假设给定簇与,分别表示簇 i 与簇 j 中样本的数量,则平均距离为:
AGNES 算法流程
AGNES 算法是一种自底向上聚合的层次聚类算法,它先会将数据集中的每个样本看作一个初始簇,然后在算法运行的每一步中找出距离最近的两个簇进行合并,直至达到预设的簇的数量。
举个例子,现在先要将西瓜数据聚成两类,数据如下表所示:
| 编号 | 体积 | 重量 |
|---|---|---|
| 1 | 1.2 | 2.3 |
| 2 | 3.6 | 7.1 |
| 3 | 1.1 | 2.2 |
| 4 | 3.5 | 6.9 |
| 5 | 1.5 | 2.5 |
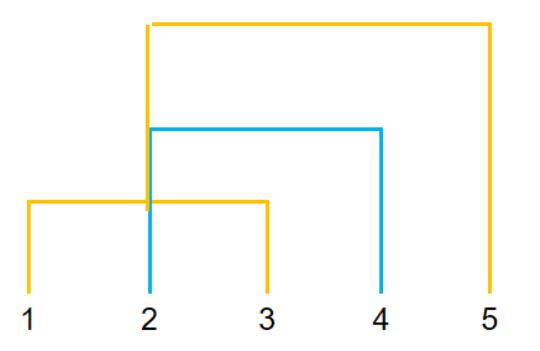
一开始,每个样本都看成是一个簇( 1 号样本看成是 1 号簇, 2 号样本看成是 2 号簇,..., 5 号样本看成是 5 号簇),假设簇的集合为 C=[[1], [2], [3], [4], [5]] 。
假设使用簇间最小距离来度量两个簇之间的远近,从表中可以看出 1 号簇与 3 号簇的簇间最小距离最小。因此需要将 1 号簇和 3 号簇合并,那么此时簇的集合 C=[[1, 3], [2], [4], [5]]。
然后继续看这 4 个簇中哪两个簇之间的最小距离最小,我们发现 2 号簇与 4 号簇的最小距离最小,因此我们要进行合并,合并之后 C=[[1, 3], [2, 4], [5]]。
然后继续看这 3 个簇中哪两个簇之间的最小距离最小,我们发现 5 号簇与 [1, 3] 簇的最小距离最小,因此我们要进行合并,合并之后 C=[[1, 3, 5], [2, 4]]。
这个时候 C 中只有两个簇了,达到了我们的预期目标(想要聚成两类),所以算法停止。算法停止后会发现,我们已经将 5 个西瓜,聚成了两类,一类是小西瓜,另一类是大西瓜。
如果将整个聚类过程中的合并,与合并的次序可视化出来,就能看出为什么说 AGNES 是自底向上的层次聚类算法了。
所以 AGNES 伪代码如下:
#假设数据集为D,想要聚成的簇的数量为k
def AGNES(D, k):
#C为聚类结果
C = []
#将每个样本看成一个簇
for d in D:
C.append(d)
#C中簇的数量
q=len(C)
while q > k:
寻找距离最小的两个簇a和b
将a和b合并,并修改C
q = len(C)
return C