2.1 kNN

kNN算法其实是众多机器学习算法中最简单的一种，因为该算法的思想完全可以用8个字来概括：“近朱者赤，近墨者黑”。

2.1.1 kNN算法解决分类问题

假设现在有这样的一个样本空间(由样本组成的一个空间)，该样本空间里有宅男和文艺青年这两个类别，其中红圈表示宅男，绿圈表示文艺青年。如下图所示：

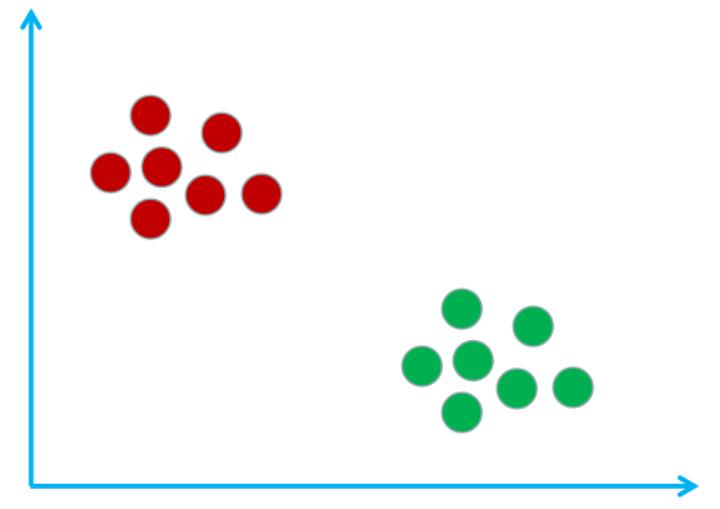
其实构建出这样的样本空间的过程就是kNN算法的训练过程。可想而知kNN算法是没有训练过程的，所以kNN算法属于懒惰学习算法。

假设我在这个样本空间中用黄圈表示，如下图所示：

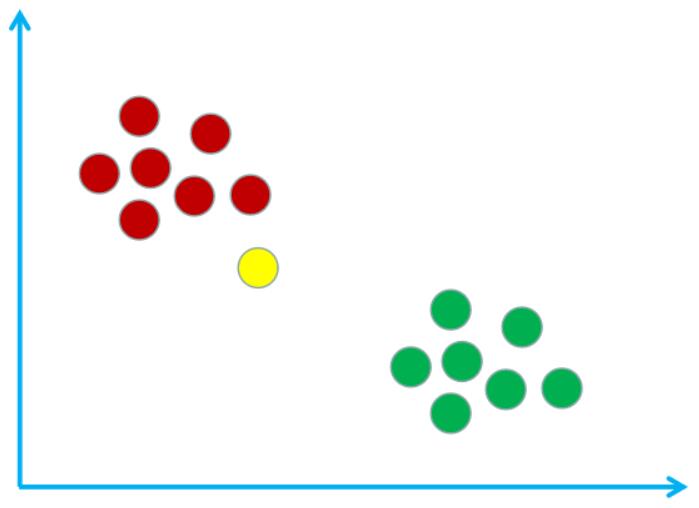
现在使用kNN算法来鉴别一下我是宅男还是文艺青年。首先需要计算我与样本空间中所有样本的距离。假设计算得到的距离表格如下：

样本编号	1	2	...	13	14
标签	宅男	宅男	...	文艺青年	文艺青年
距离	11.2	9.5	...	23.3	37.6

然后找出与我距离最小的k个样本(k是一个超参数，需要自己设置，一般默认为5)，假设与我离得最近的5个样本的标签和距离如下：

样本编号	4	5	6	7	8
标签	宅男	宅男	宅男	宅男	文艺青年
距离	11.2	9.5	7.7	5.8	15.2

最后只需要对这5个样本的标签进行统计，并将票数最多的标签作为预测结果即可。如上表中，宅男是4票，文艺青年是1票，所以我是宅男。

注意：有的时候可能会有票数一致的情况，比如k = 4时与我离得最近的样本如下：

样本编号	4	9	11	13
标签	宅男	宅男	文艺青年	文艺青年
距离	4.2	9.5	7.7	5.8

可以看出宅男和文艺青年的比分是2 : 2，那么可以尝试将属于宅男的2个样本与我的总距离和属于文艺青年的2个样本与我的总距离进行比较。然后选择总距离最小的标签作为预测结果。在这个例子中预测结果为文艺青年(宅男的总距离为4.2 + 9.5，文艺青年的总距离为7.7 + 5.8)。

很明显，刚刚使用kNN算法解决了一个分类问题，那kNN算法能解决回归问题吗？当然可以！

在使用kNN算法解决回归问题时的思路和解决分类问题的思路基本一致，只不过预测标签值是多少的的时候是将距离最近的k个样本的标签值加起来再算个平均，而不是投票。例如离待预测样本最近的5个样本的标签如下：

样本编号	4	9	11	13	15
标签	1.2	1.5	0.8	1.33	1.19

所以待预测样本的标签为：(1.2+1.5+0.8+1.33+1.19)/5=1.204