2.7 KiB
多分类学习
现实中常遇到多分类学习任务。有些二分类算法可以直接推广到多分类,但在更多情形下,我们是基于一些策略,利用二分类算法来解决多分类问题。例如:OvO、OvR。
OvO
假设现在训练数据集的分布如下图所示(其中A,B,C代表训练数据的类别):
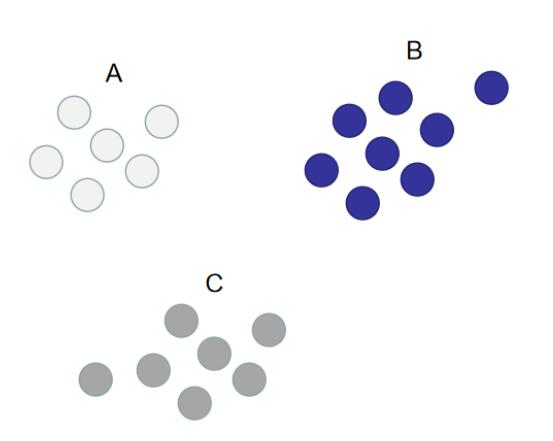
如果想要使用逻辑回归算法来解决这种3分类问题,可以使用OvO。OvO(One Vs One)是使用二分类算法来解决多分类问题的一种策略。从字面意思可以看出它的核心思想就是一对一。所谓的“一”,指的是类别。而“对”指的是从训练集中划分不同的两个类别的组合来训练出多个分类器。
划分的规则很简单,就是组合($C_n^2$,其中n表示训练集中类别的数量,在这个例子中为3)。如下图所示(其中每一个矩形框代表一种划分):
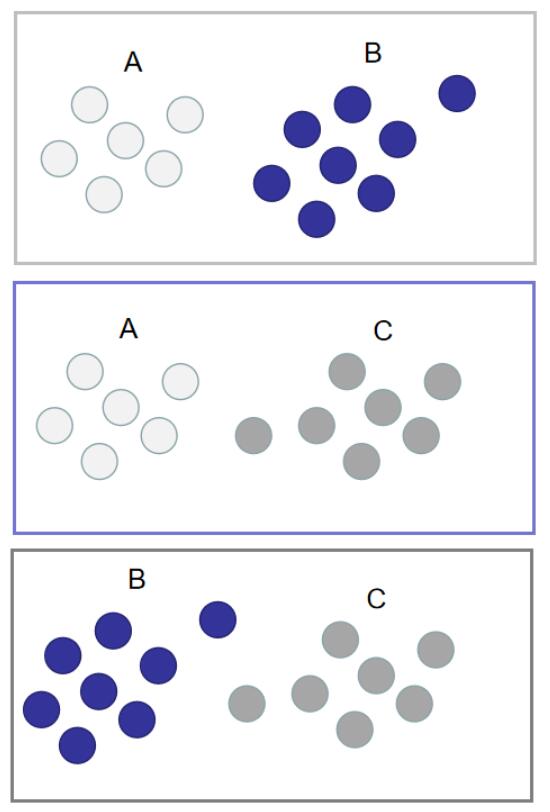
分别用这3种划分,划分出来的训练集训练二分类分类器,就能得到3个分类器。此时训练阶段已经完毕。如下图所示:
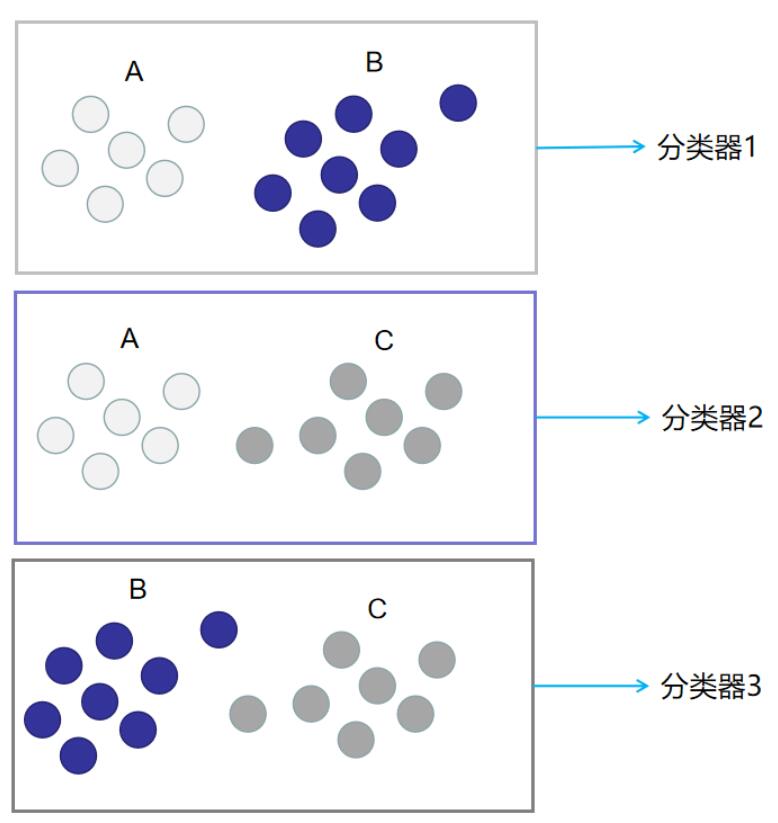
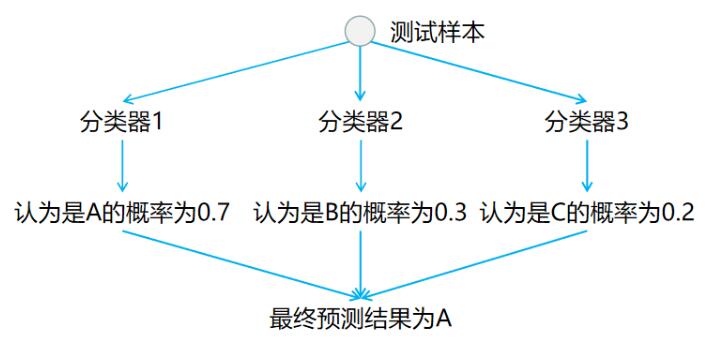
在预测阶段,只需要将测试样本分别扔给训练阶段训练好的3个分类器进行预测,最后将3个分类器预测出的结果进行投票统计,票数最高的结果为预测结果。如下图所示:
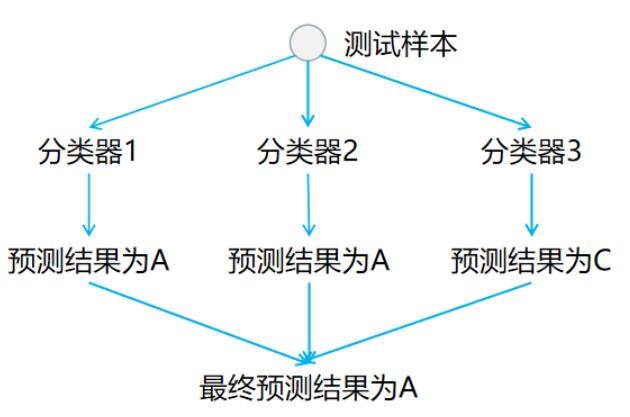
OvR
如果想要使用逻辑回归算法来解决这种3分类问题,可以使用OvR。OvR(One Vs Rest)是使用二分类算法来解决多分类问题的一种策略。从字面意思可以看出它的核心思想就是一对剩余。一对剩余的意思是当要对n种类别的样本进行分类时,分别取一种样本作为一类,将剩余的所有类型的样本看做另一类,这样就形成了n个二分类问题。所以和OvO一样,在训练阶段需要进行划分。
划分也很简单,如下图所示:
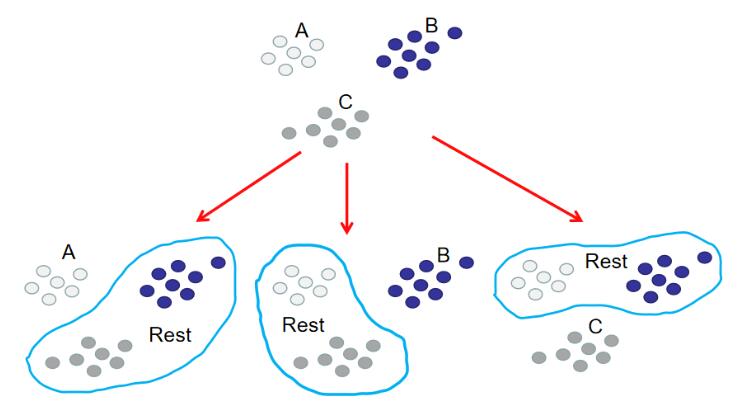
分别用这3种划分,划分出来的训练集训练二分类分类器,就能得到3个分类器。此时训练阶段已经完毕。如下图所示:
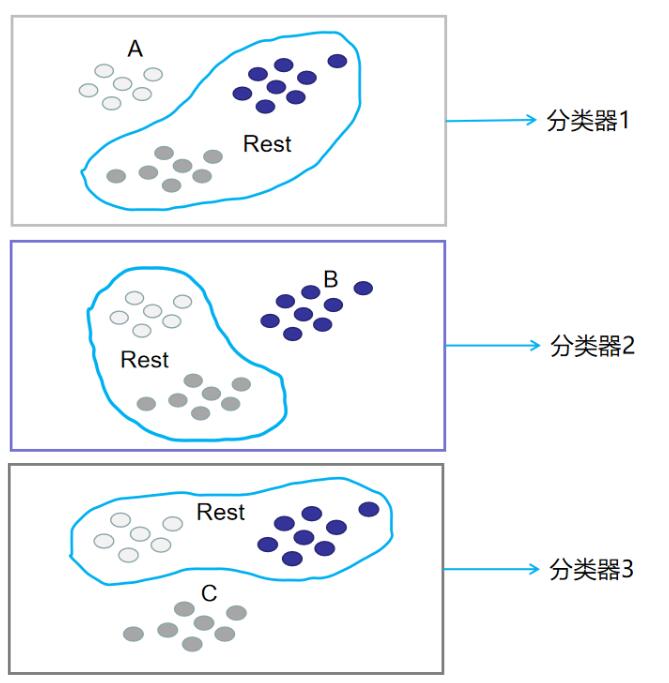
在预测阶段,只需要将测试样本分别扔给训练阶段训练好的3个分类器进行预测,最后选概率最高的类别作为最终结果。如下图所示: