5.1 KiB
2.6 随机森林
既然有决策树,那有没有用多棵决策树组成森林的算法呢?有!那就是随机森林。随机森林是一种叫Bagging的算法框架的变体。所以想要理解随机森林首先要理解Bagging。
2.6.1 Bagging
什么是Bagging
Bagging 是 Bootstrap Aggregating 的英文缩写,刚接触的您不要误认为 Bagging 是一种算法,Bagging 是集成学习中的学习框架, Bagging 是并行式集成学习方法。大名鼎鼎的随机森林算法就是在Bagging的基础上修改的算法。
** Bagging 方法的核心思想就是三个臭皮匠顶个诸葛亮**。如果使用 Bagging 解决分类问题,就是将多个分类器的结果整合起来进行投票,选取票数最高的结果作为最终结果。如果使用 Bagging 解决回归问题,就将多个回归器的结果加起来然后求平均,将平均值作为最终结果。
那么 Bagging 方法为什么如此有效呢,举个例子。狼人杀我相信您应该玩过,在天黑之前,村民们都要根据当天所发生的事和别人的发现来投票决定谁可能是狼人。
如果我们将每个村民看成是一个分类器,那么每个村民的任务就是二分类,假设 $h_i(x)表示第i个村民认为x是不是狼人(-1代表不是狼人,1 代表是狼人),f(x)表示x 真正的身份(是不是狼人),\epsilon表示为村民判断错误的错误率。则有P(h_i(x)\neq f(x))=\epsilon$。
根据狼人杀的规则,村民们需要投票决定天黑前谁是狼人,也就是说如果有超过半数的村民投票时猜对了,那么这一轮就猜对了。那么假设现在有 $T 个村民,H(x)表示投票后最终的结果,则有H(x)=sign(\sum_{i=1}^Th_i(x))$。
现在假设每个村民都是有主见的人,对于谁是狼人都有自己的想法,那么他们的错误率也是相互独立的。那么根据Hoeffding不等式可知,$H(x)$ 的错误率为:
P(H(x)\neq f(x))=\sum_{k=0}^{T/2}C_T^k(1-\epsilon)^k\epsilon ^{T-k} \leq exp(-\frac{1}{2}T(1-2\epsilon)^2)
根据上式可知,如果 $5个村民,每个村民的错误率为0.33,那么投票的错误率为0.749;如果20个村民,每个村民的错误率为0.33,那么投票的错误率为0.315;如果50个村民,每个村民的错误率为0.33,那么投票的错误率为0.056;如果100个村民,每个村民的错误率为0.33,那么投票的错误率为0.003$ 。从结果可以看出,村民的数量越大,那么投票后犯错的错误率就越小。这也是Bagging性能强的原因之一。
Bagging方法如何训练
Bagging 在训练时的特点就是随机有放回采样和并行。
随机有放回采样: 假设训练数据集有 $m条样本数据,每次从这m条数据中随机取一条数据放入采样集,然后将其返回,让下一次采样有机会仍然能被采样。然后重复m次,就能得到拥有m条数据的采样集,该采样集作为 **Bagging** 的众多分类器中的一个作为训练数据集。假设有T个分类器(随便什么分类器),那么就重复T此随机有放回采样,构建出T个采样集分别作为T$ 个分类器的训练数据集。
并行: 假设有 $10 个分类器,在**Boosting**中,1 号分类器训练完成之后才能开始2$ 号分类器的训练,而在Bagging中,分类器可以同时进行训练,当所有分类器训练完成之后,整个Bagging的训练过程就结束了。
Bagging训练过程如下图所示:
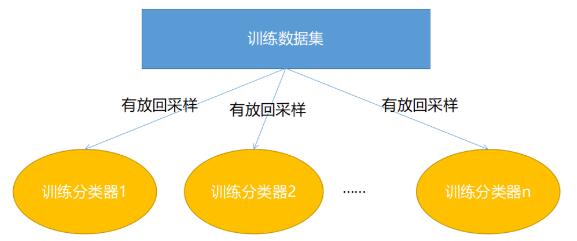
Bagging方法如何预测
Bagging在预测时非常简单,就是投票!比如现在有 $5个分类器,有3个分类器认为当前样本属于A 类,1个分类器认为属于B 类,1个分类器认为属于C类,那么**Bagging**的结果会是A类(因为A$ 类的票数最高)。
Bagging预测过程如下图所示:
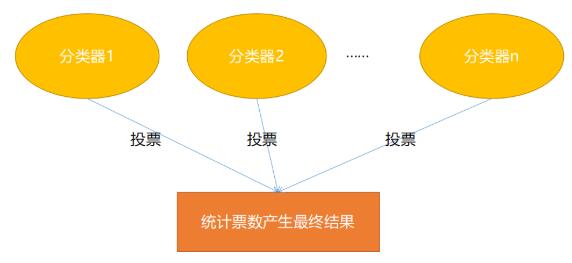
2.6.2 随机森林
随机森林是Bagging的一种扩展变体,随机森林的训练过程相对与Bagging的训练过程的改变有:
- 基学习器:Bagging的基学习器可以是任意学习器,而随机森林则是以决策树作为基学习器。
- 随机属性选择:假设原始训练数据集有
$10个特征,从这10个特征中随机选取k个特征构成训练数据子集,然后将这个子集作为训练集扔给决策树去训练。其中k的取值一般为log2$ (特征数量)。
这样的改动通常会使得随机森林具有更加强的泛化性,因为每一棵决策树的训练数据集是随机的,而且训练数据集中的特征也是随机抽取的。如果每一棵决策树模型的差异比较大,那么就很容易能够解决决策树容易过拟合的问题。