2.7 KiB
3.2 回归模型性能评估指标
3.2.1 MSE
MSE(Mean Squared Error)叫做均方误差,其实就是线性回归的损失函数。公式如下:
\frac{1}{m}\sum_{i=1}^m(y^i-p^i)^2
其中$y^i表示第`i`个样本的真实标签,p^i$表示模型对第i个样本的预测标签。线性回归的目的就是让损失函数最小。那么模型训练出来了,我们在测试集上用损失函数来评估模型就行了。
3.2.2 RMSE
RMSE(Root Mean Squard Error)均方根误差,公式如下:
\sqrt{\frac{1}{m}\sum_{i=1}^m(y^i-p^i)^2}
RMSE其实就是MSE开个根号。有什么意义呢?其实实质是一样的。只不过用于数据更好的描述。
例如:要做房价预测,每平方是万元,我们预测结果也是万元。那么差值的平方单位应该是千万级别的。那我们不太好描述自己做的模型效果。怎么说呢?我们的模型误差是多少千万?于是干脆就开个根号就好了。我们误差的结果就跟我们数据是一个级别的了,在描述模型的时候就说,我们模型的误差是多少万元。
3.2.3 MAE
MAE(Mean Aboslute Error),公式如下:
\frac{1}{m}\sum_{i=1}^m|y^i-p^i|
MAE虽然不作为损失函数,确是一个非常直观的评估指标,它表示每个样本的预测标签值与真实标签值的L1距离。
3.2.4 R-Squared
上面的几种衡量标准针对不同的模型会有不同的值。比如说预测房价 那么误差单位就是万元。数子可能是3,4,5之类的。那么预测身高就可能是0.1,0.6之类的。没有什么可读性,到底多少才算好呢?不知道,那要根据模型的应用场景来。看看分类算法的衡量标准就是正确率,而正确率又在 0~1之间,最高百分之百。最低0。如果是负数,则考虑非线性相关。很直观,而且不同模型一样的。那么线性回归有没有这样的衡量标准呢?
R-Squared就是这么一个指标,公式如下:
R^2=1-\frac{\sum_i(p^i-y^i)^2}{\sum_i(y_{mean}^i-y^i)^2}
其中$y_{mean}$表示所有测试样本标签值的均值。为什么这个指标会有刚刚我们提到的性能呢?我们分析下公式:
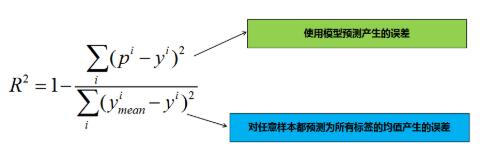
其实分子表示的是模型预测时产生的误差,分母表示的是对任意样本都预测为所有标签均值时产生的误差,由此可知:
-
R^2 \leq1 -
当我们的模型性能跟基模型性能相同时,取
0。 -
如果为负数,则说明我们训练出来的模型还不如基准模型,此时,很有可能我们的数据不存在任何线性关系。