pt5jvslni/Chapter3/生成多项式特征.md

3.5 数据预处理常用技巧---生成多项式特征

引例

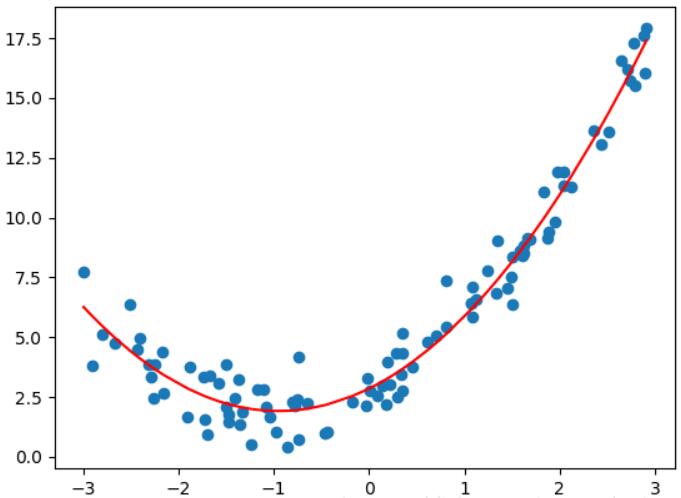
假设现在给了你一份数据，数据的分布如下图所示(其中横轴代表神秘特征X的值，纵轴代表与X所对应的目标值Y，也就是说纵轴的值可以根据X以及一种映射关系计算出来)：

我想让你根据X来将Y算出来，此时，你观察数据的分布，认为数据的分布有点像一条直线，所以你可能会使用一条直线来来表示这些数据的分布，如下图中红色的直线：

但是你会发现，红色的直线好像并不能很好的表示数据的分布，毕竟数据的分布像是一个弯弯的勾号，如果能根据特征X，使得这条直线能“打勾”就好了。如下图所示：

这个时候，我们就可以试试生成多项式特征了。即将原来的“直线”给“掰弯”。

使用sklearn来生成多项式特征

在sklearn中通过PolynomialFeatures来生成多项式特征，使用方法如下：

import numpy as np
# 导入PolynomialFeatures类
from sklearn.preprocessing import PolynomialFeatures

# 定义数据:
# [[0, 1]
# [2, 3]
# [4, 5]]
data = np.arange(6).reshape(3, 2)

# 实例化PolynomialFeatures的对象，多项式的阶为2阶
poly = PolynomialFeatures(degree=2)

# 添加多项式特征
data = poly.fit_transform(data)

# 添加之后的结果
>>>data
array([[ 1.,  0.,  1.,  0.,  0.,  1.],
       [ 1.,  2.,  3.,  4.,  6.,  9.],
       [ 1.,  4.,  5., 16., 20., 25.]])

你会看到原始数据中只有 2 个特征，而添加完多项式特征之后，特征数量增加到了 6 个。这是因为在生成多项式特征时会将原始的两个特征(x_1, x_2)，先扩展成(1, x_1, x_2)，记为 X ，然后将两个 X 中的元素两两相乘，相乘后会得到$1, x_1, x_2, x_1x_2, x_1^2, x_2^2$，即转换过程如下图所示：

所以特征数量会增加到 6 个。但是在一些情况下，我们只需要特征间的交互项，这可以通过设置 interaction_only=True来得到:

import numpy as np
# 导入PolynomialFeatures类
from sklearn.preprocessing import PolynomialFeatures

# 定义数据:
# [[0, 1]
# [2, 3]
# [4, 5]]
data = np.arange(6).reshape(3, 2)

# 实例化PolynomialFeatures的对象，多项式的阶为2阶，并只保留交叉项
poly = PolynomialFeatures(degree=2, interaction_only=True)

# 添加多项式特征
data = poly.fit_transform(data)

# 添加之后的结果
>>>data
array([[ 1.,  0.,  1.,  0.],
       [ 1.,  2.,  3.,  6.],
       [ 1.,  4.,  5., 20.]])

特征转换情况如下：

所以interaction_only为True时，特征的数量只增加到了 4 。