You can not select more than 25 topics
Topics must start with a letter or number, can include dashes ('-') and can be up to 35 characters long.
3.1 KiB
3.1 KiB
4.2 k近邻算法原理
古人云:“近朱者赤,近墨者黑”。意思是说如果一个人身边的朋友中坏人比较多,那么这个人很可能也是坏人,如果身边的朋友中好人比较多,那么他很可能也是个好人。其实k近邻算法的核心思想就是这一句古话。
如上图,当k=3时离绿色的圆最近的三个样本中,有两个红色的三角形,一个蓝色的正方形,则此时绿色的圆应该分为红色的三角形这一类。
也就是说,如果三角形是好人,正方形是坏人,那么绿色的圆就是好人,因为与绿色的圆关系最紧密的三个人中有两个是好人。
而当k=5时,离绿色的圆最近的五个样本中,有两个红色的三角形,三个蓝色的正方形,则此时绿色的圆应该分为蓝色的正方形这一类。
同样,如果三角形是好人,正方形是坏人,那么绿色的圆就是坏人,因为与绿色的圆关系最紧密的五个人中有三个是坏人。
OK,现在我们已经知道,如何判别一个样本属于哪个类型,主要是看离它最近的几个样本中哪个类型的数量最多,则该样本属于数量最多的类型。这里,存在两个问题:
- 何为最近
- 如果有两个类型的样本数一样且最多,那么最终该样本应该属于哪个类型
距离度量
关于何为最近,大家应该自然而然就会想到可以用两个样本之间的距离大小来衡量,我们常用的有两种距离:
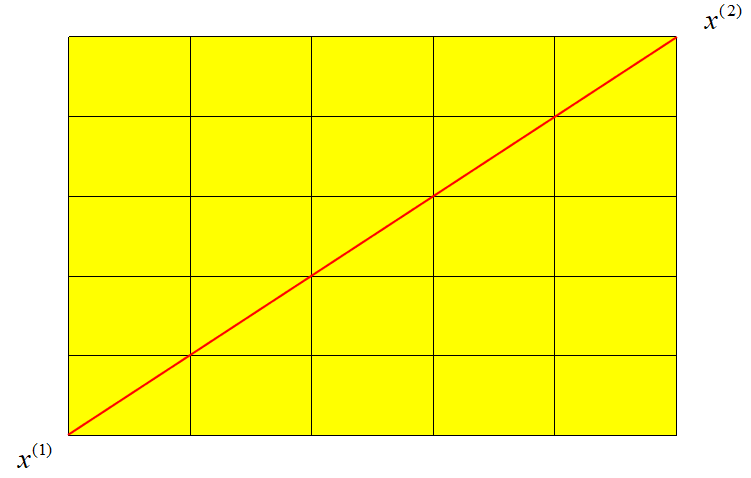
- 欧氏距离:欧氏距离是最容易直观理解的距离度量方法,我们小学、初中和高中接触到的两个点在空间中的距离一般都是指欧氏距离。
二维平面上欧式距离计算公式:
d_{12} = \sqrt{(x^{(1)}_1-x^{(2)}_1)^2+(x^{(1)}_2-x^{(2)}_2)^2}
n维平面上欧氏距离计算公式:
d_{12}=\sqrt{\sum\limits_{i=1}^n(x^{(1)}_i-x^{(2)}_i)^2}
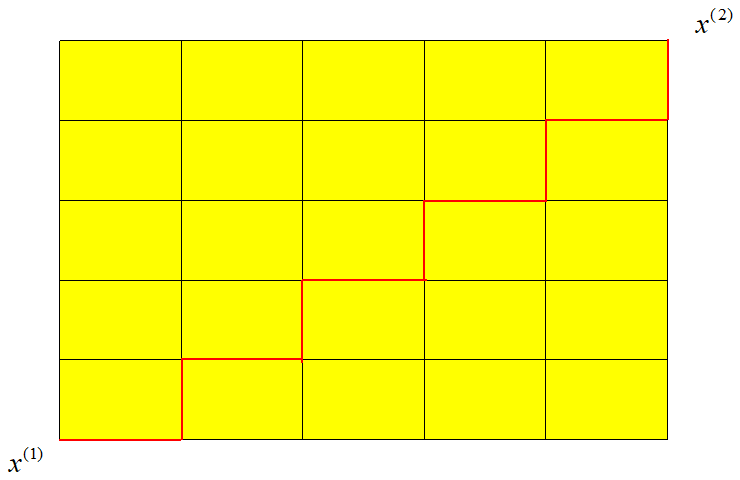
- 曼哈顿距离:顾名思义,在曼哈顿街区要从一个十字路口开车到另一个十字路口,驾驶距离显然不是两点间的直线距离。这个实际驾驶距离就是“曼哈顿距离”。曼哈顿距离也称为“城市街区距离”。
二维平面上曼哈顿距离计算公式:
d_{12}=|x^{(1)}_1-x^{(2)}_1|+|x^{(1)}_2-x^{(2)}_2|
n维平面上曼哈顿计算公式:
d_{12}=\sum\limits_{i=1}^n|x^{(1)}_i-x^{(2)}_i|
加权投票
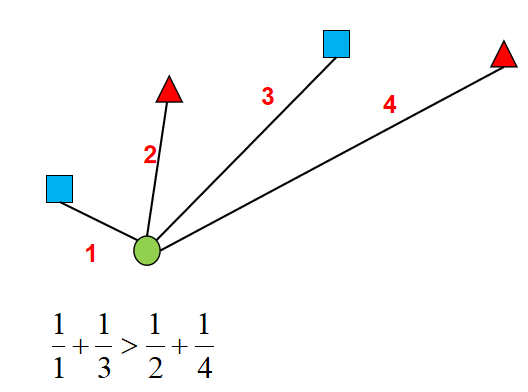
k近邻算法最后决定样本属于哪个类别,其实好比就是在投票,哪个类别票数多,则该样本属于哪个类别。而如果出现票数相同的情况,我们可以给每一票加上一个权重,用来表示每一票的重要性,这样就可以解决票数相同的问题了。很明显,距离越近的样本所投的一票应该越重要,此时我们可以将距离的倒数作为权重赋予每一票。
如上图,虽然蓝色正方形与红色三角形数量一样,但是根据加权投票的规则,绿色的圆应该属于蓝色正方形这个类别。