pt5jvslni/Chapter7/k-均值算法原理.md

7.2 k-均值算法原理

假设我们有k个簇：(c_1,c_2,...,c_k)

则我们的目的就是使的簇内的每个点到簇的质心的距离最小，即最小化平方误差MSE：

\sum\limits_{i=1}^k\sum\limits_{x\in c_i}(x-u_i)^2

其中，$u_i$为质心，表达式为：

\frac{1}{|c_i|}\sum\limits_{x\in c_i}x

|c_i|

想要直接求得最小值是非常困难的，通常我们使用启发式的迭代方法，过程如下图：

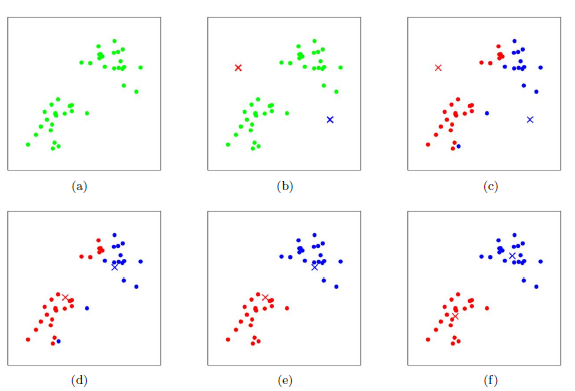
• 图b:假设k=2，我们最开始先随机初始2个质心(红色与蓝色的点)。
• 图c:计算每个样本到两个质心的距离，并将其归为与其距离最近的质心那个簇。
• 图d:更新质心，我们可以看到，红色与蓝色的点位置有了变化。
• 图e:重新计算样本到质心距离，并重新划分样本属于哪个簇。
• 图f:直到质心位置变换小于阈值或者达到迭代次数的最大值时停止迭代。

所以该算法的伪代码如下：

随机初始化k个质心
设置最大迭代次数
设置质心变化的最小阈值
while 当前迭代次数 < 最大迭代次数:
    计算每个样本分别到k个质心的距离
    对每个样本打上标记，标记为离哪个质心最近
    按照质心计算公式计算出k个新质心
    if 新质心与老质心的距离 < 质心变化的最小阈值:
        break

此时样本上的标记就代表了样本属于k个簇中的哪个簇，而k个质心表示k个簇的中心点