3.8 KiB
9.2 PageRank算法原理
最简单的场景
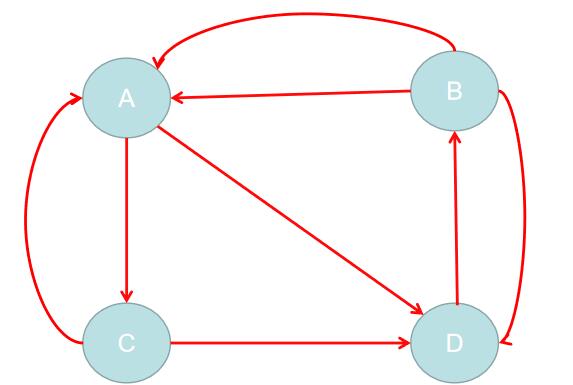
互联网中的网页可以看出是一个有向图,其中网页是结点,如果网页A有链接到网页B,则存在一条有向边A->B,下面是一个简单的示例:
这个例子中只有四个网页,如果当前在 A 网页,那么悠闲的上网者将会各以 1/3 的概率跳转到 B、C、D,这里的 3 表示 A 有 3 条出路,如果一个网页有 k 条出路,那么跳转任意一个出路上的概率是 1/k,同理 D 到 B、C 的概率各为 1/2 ,而 B 到 C 的概率为 0。一般用转移矩阵表示上网者的跳转概率,如果用 n 表示网页的数目,则转移矩阵 M 是一个 n 阶的方阵;如果网页 j 有 k 个出路,那么对每一个出链指向的网页 i,有 M[i][j]=1/k,而其他网页的 M[i][j]=0。上面示例图对应的转移矩阵如下:
一开始,假设上网者在每一个网页的概率都是相等的,即 1/n ,于是初始的概率分布就是一个所有值都为 1/n 的 n 维列向量 V0,用 V0 去右乘转移矩阵 M ,就得到了第一步之后上网者的概率分布向量 V1, 下面是V1 的计算过程:
得到了 V1 后,再用 V1 去右乘 M 得到 V2 ,一直下去,最终 V 会收敛,即 Vn=MV(n-1),不断的迭代,最终 V=[3/9,2/9,2/9,2/9]。所以如果想要向该上网者推荐一个网页,那么就会推荐网页 A。因为它的概率最高。
更复杂的场景
上述上网者的行为是一个马尔科夫过程,要满足收敛性,需要具备一个条件:图是强连通的,即从任意网页可以到达其他任意网页。
然而,互联网上的网页不满足强连通的特性,因为有一些网页不指向任何网页,如果按照上面的计算,上网者到达这样的网页后便走投无路、四顾茫然,导致前面累计得到的转移概率被清零,这样下去,最终的得到的概率分布向量所有元素几乎都为 0 。假设我们把上面图中 C 到 A 的链接丢掉, C 变成了一个终止点。
对应的转移矩阵 M 为:
这样一个转移矩阵一直迭代下去的话会发现 V=[0,0,0,0]。
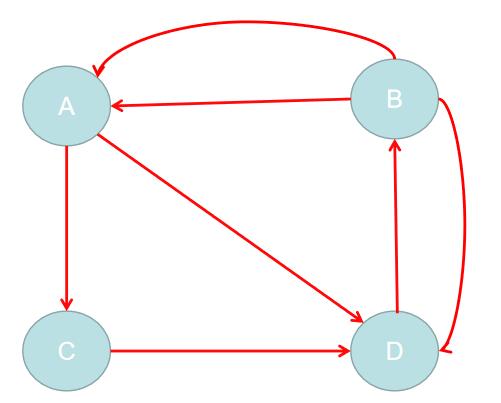
当然,还有更加复杂的场景,例如有些网页不存在指向其他网页的链接,但存在指向自己的链接。如下图所示:
上网者跑到 C 网页后,就像陷入了漩涡,再也不能从 C 中出来,将最终导致概率分布值全部转移到 C 上来,这使得其他网页的概率分布值为 0 ,从而整个网页排名就失去了意义。
怎样解决复杂场景的问题
上面过程,我们忽略了一个问题,那就是上网者是一个悠闲的上网者,而不是一个愚蠢的上网者,我们的上网者是聪明而悠闲,他悠闲,漫无目的,总是随机的选择网页,他聪明,在走到一个终结网页或者一个陷阱网页(比如图中的 C ),不会傻傻的干着急,他会在浏览器的地址随机输入一个地址,当然这个地址可能又是原来的网页,但这里给了他一个逃离的机会,让他离开这万丈深渊。模拟聪明而又悠闲的上网者,对算法进行改进,每一步,上网者可能都不想看当前网页了,不看当前网页也就不会点击上面的连接,而上悄悄地在地址栏输入另外一个地址,而在地址栏输入而跳转到各个网页的概率是 1/n 。假设上网者每一步查看当前网页的概率为 a ,那么他从浏览器地址栏跳转的概率为 (1-a) ,于是迭代公式转化为:
V'=\alpha MV+(1-\alpha)V
假设场景如下图所示:
很显然,该图所对应的转移矩阵 M 为如下所示:
那么假设上网者查看当前网页的概率为 0.8 ,则根据公式可知:
然后一直迭代下去,当收敛时可知 V=[3/9,2/9,2/9,2/9]。