pt5jvslni/Chapter3/非线性变换.md

3.3 非线性变换

为什么要非线性转换

对于大多数数据挖掘算法来说，如果特征不服从或者近似服从标准正态分布（即，零均值、单位标准差的正态分布）的话，算法的表现会大打折扣。非线性转换就是将我们的特征映射到均匀分布或者高斯分布(即正态分布)。

映射到均匀分布

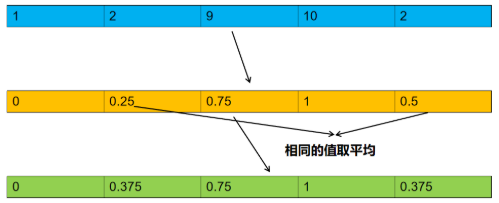
相比线性缩放，该方法不受异常值影响，它将数据映射到了零到一的均匀分布上，将最大的数映射为1，最小的数映射为0。其它的数按从小到大的顺序均匀分布在0到1之间，如有相同的数则取平均值，如数据为np.array([[1],[2],[3],[4],[5]])则经过转换为：np.array([[0],[0.25],[0.5],[0.75],[1]])，数据为np.array([[1],[2],[9],[10],[2]])则经过转换为：np.array([[0],[0.375],[0.75],[1.0],[0.375]])。第二个例子具体过程如下图：

在sklearn中使用QuantileTransformer方法实现，用法如下：

from sklearn.preprocessing import QuantileTransformer
import numpy as np

data = np.array([[1],[2],[3],[4],[5]])
quantile_transformer = QuantileTransformer(random_state=666)
data = quantile_transformer.fit_transform(data)

>>>data
array([[0.  ],
       [0.25],
       [0.5 ],
       [0.75],
       [1.  ]])

映射到高斯分布

映射到高斯分布是为了稳定方差，并最小化偏差。在最新版sklearn 0.20.x中PowerTransformer现在有两种映射方法，Yeo-Johnson映射，公式如下：

x_i^{(\lambda)} = \begin{cases}
[(x_i+1)^\lambda-1],if \lambda\neq0,x_i\geq0\\
\ln(x_i)+1,if\lambda=0,x_i\geq0\\
-[(-x_i+1)^{2-\lambda}-1]/(2-\lambda),if\lambda\neq2,x_i<0\\
-\ln(-x_i+1),if\lambda=2,x_i<0
\end{cases}

Box-Cox映射，公式如下：

x_i^{(\lambda)} = \begin{cases}
\frac{x_i^\lambda-1}{\lambda},if\lambda\neq0\\
\ln(x_i),if\lambda=0
\end{cases}

在sklearn 0.20.x中使用PowerTransformer方法实现，用法如下：

from sklearn.preprocessing import PowerTransformer
import numpy as np

data = np.array([[1],[2],[3],[4],[5]])
pt = PowerTransformer(method='box-cox', standardize=False)

data = pt.fit_transform(data)

学习平台使用的是sklearn 0.19.x，通过对QuantileTransformer设置参数output_distribution='normal'实现映射高斯分布，用法如下：

from sklearn.preprocessing import QuantileTransformer
import numpy as np

data = np.array([[1],[2],[3],[4],[5]])
quantile_transformer = QuantileTransformer(output_distribution='normal',random_state=666)
data = quantile_transformer.fit_transform(data)
data = np.around(data,decimals=3)

>>>data
array([[-5.199],
       [-0.674],
       [ 0.   ],
       [ 0.674],
       [ 5.199]])