pgi29wjsp/classification_metrics.md

分类模型性能评估指标

##准确度的缺陷

准确度这个概念相信对于大家来说肯定并不陌生，就是正确率。例如模型的预测结果与数据真实结果如下表所示：

编号	预测结果	真实结果
1	1	2
2	2	2
3	3	3
4	1	1
5	2	3

很明显，连小朋友都能算出来该模型的准确度为3/5。

那么准确对越高就能说明模型的分类性能越好吗？非也！举个例子，现在我开发了一套癌症检测系统，只要输入你的一些基本健康信息，就能预测出你现在是否患有癌症，并且分类的准确度为0.999。您认为这样的系统的预测性能好不好呢？

您可能会觉得，哇，这么高的准确度！这个系统肯定很牛逼！但是我们知道，一般年轻人患癌症的概率非常低，假设患癌症的概率为0.001 ，那么其实我这个癌症检测系统只要一直输出您没有患癌症，准确度也可能能够达到0.999。

假如现在有一个人本身已经患有癌症，但是他自己不知道自己患有癌症。这个时候用我的癌症检测系统检测发现他没有得癌症，那很显然我这个系统已经把他给坑了（耽误了治疗）。

看到这里您应该已经体会到了，一个分类模型如果光看准确度是不够的，尤其是对这种样本极度不平衡的情况（10000条健康信息数据中，只有1条的类别是患有癌症，其他的类别都是健康）。

##混淆矩阵

想进一步的考量分类模型的性能如何，可以使用其他的一些性能指标，例如精准率和召回率。但这些指标计算的基础是混淆矩阵。

继续以癌症检测系统为例，癌症检测系统的输出不是有癌症就是健康，这里为了方便，就用1表示患有癌症，0表示健康。假设现在拿10000条数据来进行测试，其中有9978条数据的真实类别是0，系统预测的类别也是0 ，有2条数据的真实类别是1却预测成了0，有12条数据的真实类别是0但预测成了1，有8条数据的真实类别是1 ，预测结果也是1。

如果我们把这些结果组成如下矩阵，则该矩阵就成为混淆矩阵。

真实\预测	0	1
0	9978	12
1	2	8

混淆矩阵中每个格子所代表的的意义也很明显，意义如下：

真实\预测	0	1
0	预测 0 正确的数量	预测 1 错误的数量
1	预测 0 错误的数量	预测 1 正确的数量

如果将正确看成是True，错误看成是False， 0看成是 Negtive，1看成是Positive。然后将上表中的文字替换掉，混淆矩阵如下：

真实\预测	0	1
0	TN	FP
1	FN	TP

因此TN表示真实类别是Negtive，预测结果也是Negtive的数量； FP表示真实类别是Negtive，预测结果是Positive的数量； FN表示真实类别是Positive，预测结果是Negtive的数量； TP表示真实类别是Positive，预测结果也是Positive的数量。

很明显，当FN和FP都等于0时，模型的性能应该是最好的，因为模型并没有在预测的时候犯错误。即如下混淆矩阵：

真实\预测	0	1
0	9978	0
1	0	22

所以模型分类性能越好，混淆矩阵中非对角线上的数值越小。

精准率

**精准率(Precision)**指的是模型预测为Positive时的预测准确度，其计算公式如下：

$$ Precisioin=\frac{TP}{TP+FP} $$

假如癌症检测系统的混淆矩阵如下：

真实\预测	0	1
0	9978	12
1	2	8

则该系统的精准率为：8/(8+12)=0.4。

0.4这个值表示癌症检测系统的预测结果中如果有100个人被预测成患有癌症，那么其中有40人是真的患有癌症。也就是说，精准率越高，那么癌症检测系统预测某人患有癌症的可信度就越高。

##召回率

**召回率(Recall)**指的是我们关注的事件发生了，并且模型预测正确了的比值，其计算公式如下：

$$ Recall=\frac{TP}{FN+TP} $$

假如癌症检测系统的混淆矩阵如下：

真实\预测	0	1
0	9978	12
1	2	8

则该系统的召回率为：8/(8+2)=0.8。

从计算出的召回率可以看出，假设有100个患有癌症的病人使用这个系统进行癌症检测，系统能够检测出80人是患有癌症的。也就是说，召回率越高，那么我们感兴趣的对象成为漏网之鱼的可能性越低。

##精准率与召回率之间的关系

假设有这么一组数据，菱形代表Positive，圆形代表Negtive 。

现在需要训练一个模型对数据进行分类，假如该模型非常简单，就是在数据上画一条线作为分类边界。模型认为边界的左边是Negtive，右边是Positive。如果该模型的分类边界向左或者向右移动的话，模型所对应的精准率和召回率如下图所示：

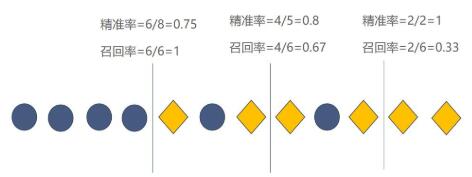
从上图可知，模型的精准率变高，召回率会变低，精准率变低，召回率会变高。

##F1 Score

上一节中提到了精准率变高，召回率会变低，精准率变低，召回率会变高。那如果想要同时兼顾精准率和召回率，这个时候就可以使用F1 Score来作为性能度量指标了。

F1 Score是统计学中用来衡量二分类模型精确度的一种指标。它同时兼顾了分类模型的准确率和召回率。F1 Score可以看作是模型准确率和召回率的一种加权平均，它的最大值是1，最小值是0 。其公式如下：

$$ F1=\frac{2*precision*recall}{precision+recall} $$

• 假设模型A的精准率为0.2，召回率为0.7，那么模型A的F1 Score为0.31111。

• 假设模型B的精准率为0.7，召回率为0.2，那么模型B的F1 Score为0.31111。

• 假设模型C的精准率为0.8，召回率为0.7，那么模型C的F1 Score为0.74667。

• 假设模型D的精准率为0.2，召回率为0.3，那么模型D的F1 Score为0.24。

从上述4个模型的各种性能可以看出，模型C的精准率和召回率都比较高，因此它的F1 Score也比较高。而其他模型的精准率和召回率要么都比较低，要么一个低一个高，所以它们的F1 Score比较低。

这也说明了只有当模型的精准率和召回率都比较高时F1 Score才会比较高。这也是F1 Score能够同时兼顾精准率和召回率的原因。

ROC曲线

ROC曲线(Receiver Operating Characteristic Curve)描述的是TPR（True Positive Rate）与 FPR（False Positive Rate）之间关系的曲线。

TPR与FPR的计算公式如下：

$$ TPR=\frac{TP}{TP+FN} $$
$$ FPR=\frac{FP}{FP+TN} $$

其中TPR的计算公式您可能有点眼熟，没错！就是召回率的计算公式。也就是说 TPR 就是召回率。所以 TPR 描述的是模型预测 Positive 并且预测正确的数量占真实类别为 Positive 样本的比例。而 FPR 描述的模型预测 Positive 并且预测错了的数量占真实类别为 Negtive 样本的比例。

和精准率与召回率一样，TPR与FPR之间也存在关系。假设有这么一组数据，菱形代表Positive，圆形代表Negtive。

现在需要训练一个逻辑回归的模型对数据进行分类，假如将从0到 1中的一些值作为模型的分类阈值。若模型认为当前数据是 Positive的概率小于分类阈值则分类为 Negtive ，否则就分类为Positive（假设分类阈值为 0.8 ，模型认为这条数据是 Positive 的概率为 0.7 ， 0.7 小于 0.8 ，那么模型就认为这条数据是 Negtive）。在不同的分类阈值下，模型所对应的TPR与FPR如下图所示（竖线代表分类阈值，模型会将竖线左边的数据分类成Negtive，竖线右边的分类成Positive）：

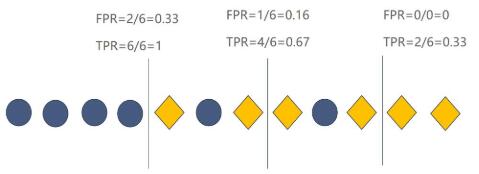
从图中可以看出，**当模型的 TPR 越高 FPR 也会越高， TPR 越低 FPR 也会越低。这与精准率和召回率之间的关系刚好相反。**并且，模型的分类阈值一但改变，就有一组对应的TPR与FPR。假设该模型在不同的分类阈值下其对应的TPR与FPR如下表所示：

TPR	FPR
0.2	0.08
0.35	0.1
0.37	0.111
0.51	0.12
0.53	0.13
0.56	0.14
0.71	0.21
0.82	0.26
0.92	0.41
0.93	0.42

若将FPR作为横轴，TPR作为纵轴，将上面的表格以折线图的形式画出来就是ROC曲线。

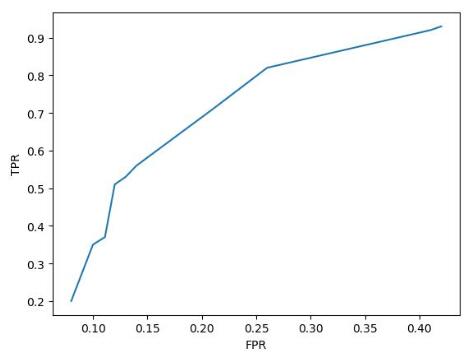
假设现在有模型A和模型B，它们的ROC曲线如下图所示(其中模型A的ROC曲线为黄色，模型B的ROC曲线为蓝色)：

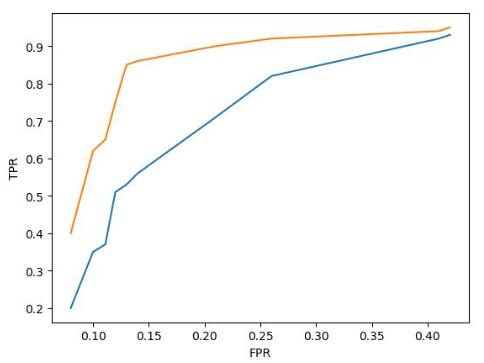
那么模型A的性能比模型B的性能好，因为模型A当FPR较低时所对应的TPR比模型B的低FPR所对应的TPR更高。由由于随着FPR的增大，TPR也会增大。所以ROC曲线与横轴所围成的面积越大，模型的分类性能就越高。而ROC曲线的面积称为AUC。

#####AUC

很明显模型的AUC越高，模型的二分类性能就越强。AUC的计算公式如下：

$$ AUC=\frac{\sum_{ie positive class}rank_i-\frac{M(M+1)}{2}}{M*N} $$

其中M为真实类别为Positive的样本数量，N为真实类别为 Negtive的样本数量。ranki代表了真实类别为Positive的样本点额预测概率从小到大排序后，该预测概率排在第几。

举个例子，现有预测概率与真实类别的表格如下所示（其中0表示 Negtive ，1表示Positive）：

编号	预测概率	真实类别
1	0.1	0
2	0.4	0
3	0.3	1
4	0.8	1

想要得到公式中的rank ，就需要将预测概率从小到大排序，排序后如下：

编号	预测概率	真实类别
1	0.1	0
3	0.3	1
2	0.4	0
4	0.8	1

排序后的表格中，真实类别为Positive只有编号为3和编号为4的数据，并且编号为3的数据排在第2 ，编号为4的数据排在第4。所以rank=[2, 4]。又因表格中真是类别为 Positive的数据有2条，Negtive的数据有2条。因此M为2，N为2。所以根据AUC的计算公式可知：

$$ AUC=\frac{(2+4)-\frac{2(2+1)}{2}}{2*2}=0.75 $$